Watson (1939) considered the following three triple integrals,

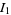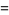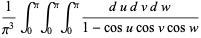			(1)
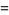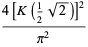			(2)
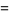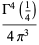			(3)
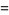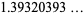			(4)
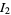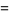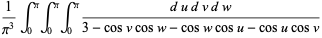			(5)
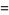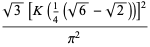			(6)
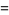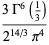			(7)
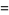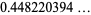			(8)
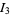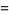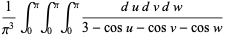			(9)
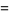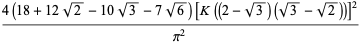			(10)
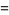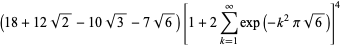			(11)
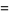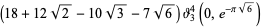			(12)
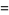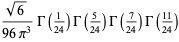			(13)
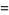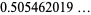			(14)

(OEIS A091670, A091671, and A091672), where 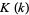 is a complete elliptic integral of the first kind,  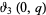is a Jacobi theta function, and  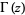is the gamma function. Analytic computation of these integrals is rather challenging, especially  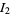and .

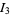Watson (1939) treats all three integrals by making the transformations

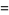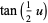			(15)
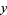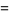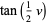			(16)
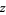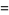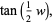			(17)

regarding , , 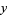and 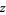 as Cartesian coordinates, and changing to polar coordinates,

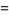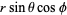			(18)
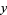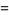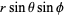			(19)
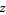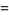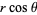			(20)

after writing .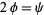

Performing this transformation on 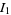 gives

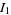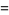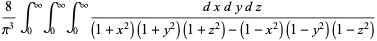			(21)
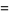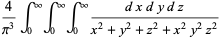			(22)
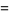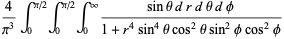			(23)
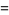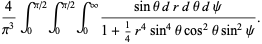			(24)

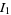 can then be directly integrated using computer algebra, although Watson (1939) used the additional transformation

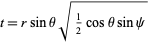(25)

to separate the integral into

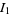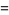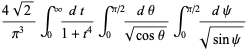			(26)
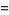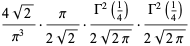			(27)
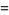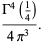			(28)

The integral 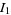 can also be done by performing one of the integrations

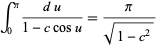(29)

with 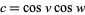 to obtain

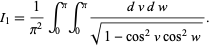(30)

Expanding using a binomial series

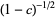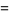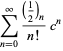			(31)
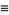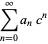			(32)

where 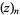 is a Pochhammer symbol and

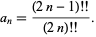(33)

Integrating gives

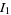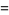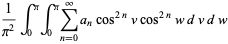			(34)
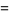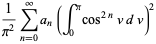			(35)
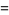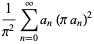			(36)
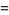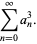			(37)

Now, as a result of the amazing identity for the complete elliptic integral of the first kind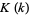 

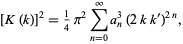(38)

where 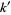 is the complementary modulus and  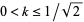(Watson 1908, Watson 1939), it follows immediately that with  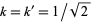(i.e., 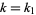, the first singular value),

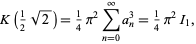(39)

so

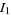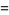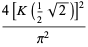			(40)
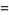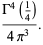			(41)

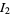 can be transformed using the same prescription to give

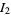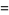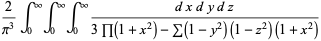			(42)
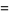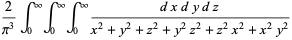			(43)
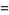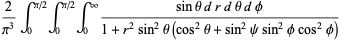			(44)
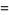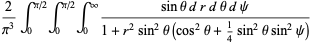			(45)
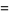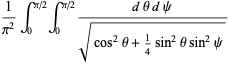			(46)
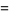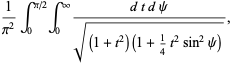			(47)

where the substitution 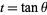 has been made in the last step. Computer algebra can return this integral in the form of a Meijer G-function

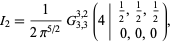(48)

but more clever treatment is needed to obtain it in a nicer form. For example, Watson (1939) notes that

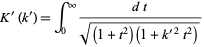(49)

immediately gives

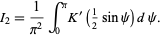(50)

However, quadrature of this integral requires very clever use of a complicated series identity for 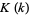 to obtain term by term integration that can then be recombined as recognized as

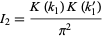(51)

(Watson 1939).

For 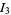, only a single integration can be done analytically, namely

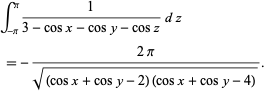(52)

It can be reduced to a single infinite sum by defining 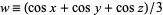 and using a binomial series expansion to write

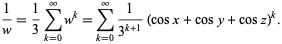(53)

But this can then be written as a multinomial series and plugged back in to obtain

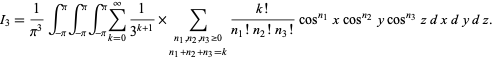(54)

Exchanging the order of integration and summation allows the integrals to be done, leading to

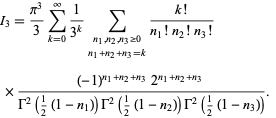(55)

Rather surprisingly, the sums over 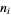 can be done in closed form, yielding

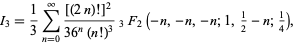(56)

where 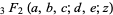 is a generalized hypergeometric function. However, this sum cannot be done in closed form.

Watson (1939) transformed the integral to

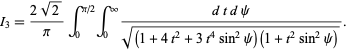(57)

However, to obtain an entirely closed form, it is necessary to do perform some analytic wizardry (see Watson 1939 for details). The fact that a closed form exists at all for this integral is therefore rather amazing.

REFERENCES:

Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006b.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Domb, C. "On Multiple Returns in the Random-Walk Problem." Proc. Cambridge Philos. Soc. 50, 586-591, 1954.

Glasser, M. L. and Zucker, I. J. "Extended Watson Integrals for the Cubic Lattices." Proc. Nat. Acad. Sci. U.S.A. 74, 1800-1801, 1977.

Joyce, G. and Zucker, I. J. "On the Evaluation of Generalized Watson Integrals." Proc. Amer. Math. Soc. 133, 71-81, 2005.

McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.

Sloane, N. J. A. Sequences A091670, A091671, and A091672 in "The On-Line Encyclopedia of Integer Sequences."

Watson G. N. "The Expansion of Products of Hypergeometric Functions." Quart. J. Pure Appl. Math. 39, 27-51, 1907.

Watson G. N. "A Series for the Square of the Hypergeometric Function." Quart. J. Pure Appl. Math. 40, 46-57, 1908.

Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.

اخر الاخبار

اخبار العتبة العباسية المقدسة

بذكرى شهادته.. جموع الزائرين تشيع النعش الرمزي للإمام الكاظم (عليه السلام) عند مرقده الطاهر في بغداد

العتبة العباسية المقدسة تنظم مجلس عزاء بذكرى شهادة الإمام الكاظم (عليه السلام)

جموع المؤمنين تشيّع النعش الرمزي للإمام الكاظم (عليه السلام) عند العتبتين المقدستين

شعبة التوجيه الديني النسوي تنظم مسابقة ميدانية بذكرى شهادة الإمام الكاظم (عليه السلام)

المزيد

الآخبار الصحية

الخبز الأسمر أم الأبيض.. أيهما أفضل لضبط سكر الدم؟

عقاقير التخسيس و"الانتحار".. الحكومة الأميركية تحسم الجدل

الهرم الغذائي الجديد.. لماذا يعد "انقلابا" في خارطة الطعام؟

لحماية ظهرك وقلبك في آن واحد.. ما وضعية النوم الصحيحة؟

المزيد

الآخبار التكنلوجية

كيف يعزز الضوء الطبيعي تفكيرك وانتباهك خلال اليوم

سابقة.. طاقم من محطة الفضاء الدولية يعود إلى الأرض مبكرا

منصات التواصل تضرّ بنفسية المراهقين… والفتيات الأكثر تأثرا

ابتكار ألماني قد يغيّر مستقبل صناعة البلاستيك

المزيد