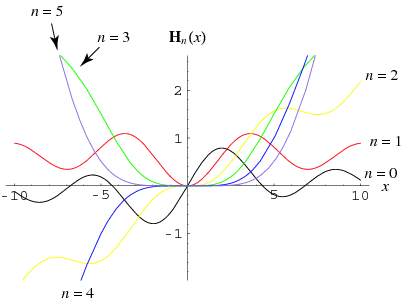
The Struve function, denoted 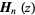 or occasionally 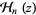, is defined as

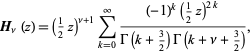(1)

where 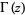 is the gamma function (Abramowitz and Stegun 1972, pp. 496-499). Watson (1966, p. 338) defines the Struve function as

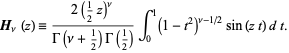(2)

The Struve function is implemented as StruveH[n, z].

The Struve function and its derivatives satisfy

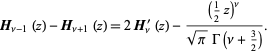(3)

For integer 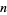, the Struve function gives the solution to

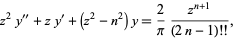(4)

where 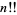 is the double factorial.

The Struve function arises in the problem of the rigid-piston radiator mounted in an infinite baffle, which has radiation impedance given by

(5)

where

			(6)
			(7)

where 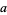 is the piston radius,  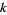is the wavenumber 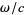,  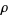is the density of the medium,  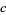is the speed of sound, 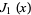is the first order Bessel function of the first kind and  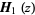is the Struve function of the first kind.

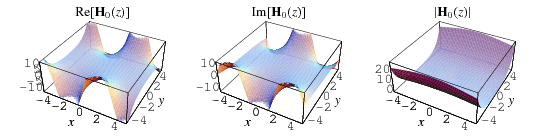
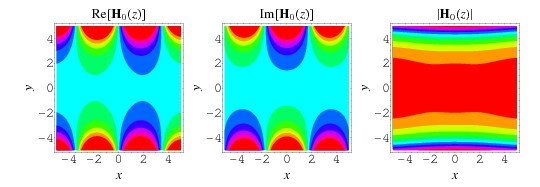
The illustrations above show the values of the Struve function 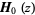 in the complex plane.

For integer orders,

			(8)
			(9)
			(10)
			(11)

(OEIS A001818 and A079484).

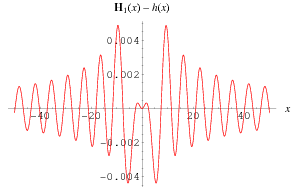
A simple approximation of 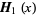 for real  is given by

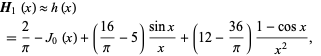(12)

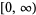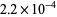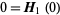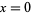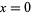with squared approximation error on  equal to  by Parseval's formula (Aarts and Janssen 2003). The right-hand side of equation (12) equals  for . The approximation error is small and decently spread-out over the whole -range, vanishes for , and reaches its maximum value at about 0.005. The maximum relative error appears to be less than 1% and decays to zero for .

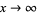For half integer orders,

			(13)
			(14)

The first few cases are

			(15)
			(16)
			(17)

REFERENCES:

Aarts, R. M. and Janssen, A. J. E. M. "Approximation of the Struve Function 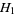 Occurring in Impedance Calculations." J. Acoust. Soc. Amer. 113, 2635-2637, 2003.

Abramowitz, M. "Tables of Integrals of Struve Functions." J. Math. Phys. 29, 49-51, 1950.

Abramowitz, M. and Stegun, I. A. (Eds.). "Struve Function 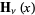." §12.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 496-498, 1972.

Apelblat, A. "Derivatives and Integrals with Respect to the Order of the Struve Functions 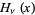 and 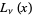." J. Math. Anal. Appl.137, 17-36, 1999.

Cook, R. K. "Some Properties of Struve Functions." J. Washington Acad. Sci. 47, 365-368, 1957.

Horton, C. W. "On the Extension of Some Lommel Integrals to Struve Functions with an Application to Acoustic Radiation." J. Math. Phys. 29, 31-37, 1950.

Horton, C. W. "A Short Table of Struve Functions and of Some Integrals Involving Bessel and Struve Functions." J. Math. Phys.29, 56-58, 1950.

Mathematical Tables Project. "Table of the Struve Functions 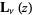 and 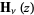." J. Math. Phys. 25, 252-259, 1946.

Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Struve Functions 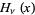 and 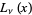." §1.4 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 24-27, 1990.

Sloane, N. J. A. Sequences A001818/M4669 and A079484 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Struve Function." Ch. 57 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 563-571, 1987.

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.