Gudermannian
المؤلف:
Beyer, W. H.
المصدر:
"Gudermannian Function." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press
الجزء والصفحة:
...
2-5-2019
1868
Gudermannian
The Gudermannian function is the odd function denoted eithe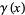r 
or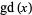 
which arises in the inverse equations for the Mercator projection. 
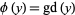expresses the latitude 
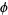in terms of the vertical position 
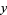in this projection, so the Gudermannian function is defined by
For real 
, this definition is also equal to
The Gudermannian is implemented in the Wolfram Language as Gudermannian[z].
The derivative of the Gudermannian is
 |
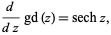(5)
|
and its indefinite integral is
![intgd(z)dz=-1/2pix+i[Li_2(-ie^x)-Li_2(ie^x)],](http://mathworld.wolfram.com/images/equations/Gudermannian/NumberedEquation2.gif) |
(6)
|
where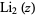 
is the dilogarithm.
It has Maclaurin series
 |
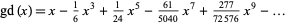(7)
|
(OEIS A091912 and A136606).
The Gudermannian connects the trigonometric and hyperbolic functions via
The Gudermannian is related to the exponential function by
(Beyer 1987, p. 164; Zwillinger 1995, p. 485).
Other fundamental identities are
 |
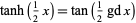(17)
|
 |
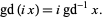(18)
|
(Zwillinger 1995, p. 485).
If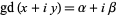 
, then
(Beyer 1987, p. 164; Zwillinger 1995, p. 530), where the last identity has been corrected.
An additional identity is given by
 |
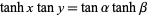(23)
|
(M. Somos, pers. comm., Apr. 15, 2006).
The Gudermannian function can also be extended to the complex plane, as illustrated above.
REFERENCES:
Beyer, W. H. "Gudermannian Function." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 164, 1987.
Robertson, J. S. "Gudermann and the Simple Pendulum." College Math. J. 28, 271-276, 1997.
Sloane, N. J. A. Sequences A091912 and A136606 in "The On-Line Encyclopedia of Integer Sequences."
Zwillinger, D. (Ed.). "Gudermannian Function." §6.9 in CRC Standard Mathematical Tables and Formulae, 31st ed. Boca Raton, FL: CRC Press, pp. 530-532, 1995.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
