Kampé de Fériet Function
المؤلف:
Appell, P
المصدر:
Sur les fonctions hypergéométriques de plusieurs variables. Paris: Gauthier-Villars, 1925.
الجزء والصفحة:
...
15-6-2019
3652
Kampé de Fériet Function
A special function generalizes the generalized hypergeometric function to two variables and includes the Appell hypergeometric function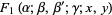 
as a special case. The Kampe de Feriet function can represent derivatives of generalized hypergeometric functions with respect to their parameters, as well as indefinite integrals of two and three Meijer G-functions. Exton and Krupnikov (1998) have derived a large collection of formulas involving this function.
Kampé de Fériet functions are written in the notation
 |
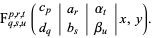(1)
|
Special cases include
 |
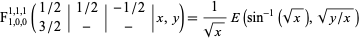(2)
|
 |
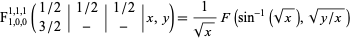(3)
|
for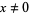 
and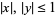 
, where 
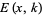is the incomplete elliptic integral of the second kind and 
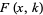is the incomplete elliptic integral of the first kind, as well as
 |
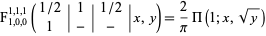(4)
|
for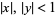 
, where 
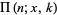is the incomplete elliptic integral of the third kind (Exton and Krupnikov 1998, p. 1). Additional identities are given by
 |
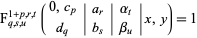(5)
|
 |
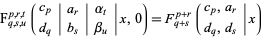(6)
|
 |
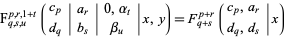(7)
|
(Exton and Krupnikov 1998, p. 3).
REFERENCES:
Appell, P. Sur les fonctions hypergéométriques de plusieurs variables. Paris: Gauthier-Villars, 1925.
Appell, P. and Kampé de Fériet, J. Fonctions hypergéométriques et hypersphériques: polynomes d'Hermite. Paris: Gauthier-Villars, 1926.
Exton, H. "The Kampé de Fériet Function." §1.3.2 in Handbook of Hypergeometric Integrals: Theory, Applications, Tables, Computer Programs. Chichester, England: Ellis Horwood, pp. 24-25, 1978.
Exton, H. Multiple Hypergeometric Functions and Applications. Chichester, England: Ellis Horwood, 1976.
Exton, H. and Krupnikov, E. D. A Register of Computer-Oriented Reduction Identities for the Kampé de Fériet Function. Draft manuscript. Novosibirsk, 1998.
Kampé de Fériet, J. La fonction hypergéométrique. Paris: Gauthier-Villars, 1937.
Ragab, F. J. "Expansions of Kampe De Feriet's Double Hypergeometric Function of Higher Order." J. reine angew. Math. 212, 113-119, 1963.
Srivastava, H. M., Karlsson, P. W. Multiple Gaussian Hypergeometric Series. Chichester, England: Ellis Horwood, 1985.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
