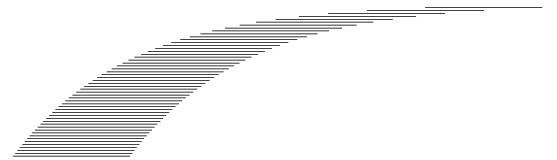
How far can a stack of 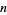 books protrude over the edge of a table without the stack falling over? It turns out that the maximum overhang possible  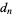for 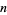 books (in terms of book lengths) is half the 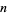th partial sum of the harmonic series.

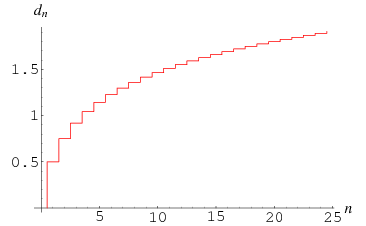
This is given explicitly by

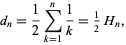(1)

where 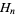 is a harmonic number. The first few values are

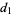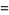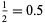			(2)
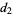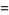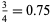			(3)
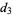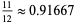			(4)
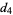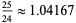			(5)

(OEIS A001008 and A002805).

When considering the stacking of a deck of 52 cards so that maximum overhang occurs, the total amount of overhang achieved after sliding over 51 cards leaving the bottom one fixed is

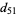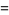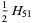			(6)
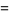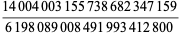			(7)
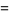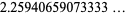			(8)

(Derbyshire 2004, p. 6).

In order to find the number of stacked books required to obtain 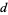 book-lengths of overhang, solve the  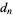equation for 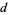, and take the ceiling function. For 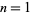, 2, ... book-lengths of overhang, 4, 31, 227, 1674, 12367, 91380, 675214, 4989191, 36865412, 272400600, ... (OEIS A014537) books are needed.

When more than one book or card can be used per level, the problem becomes much more complex. For example, using cards stacked in the shape of an oil lamp, an overhang of 10 is possible with 921 blocks (Paterson and Zwick 2006).

REFERENCES:

Boas, R. "Cantilevered Books." Amer. J. Phys. 41, 715, 1973.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 3-8, 2004.

Dickau, R. M. "The Book-Stacking Problem." http://www.prairienet.org/~pops/BookStacking.html.

Eisner, L. "Leaning Tower of the Physical Review." Amer. J. Phys. 27, 121, 1959.

Gamow, G. and Stern, M. Puzzle Math. New York: Viking, 1958.

Gardner, M. Martin Gardner's Sixth Book of Mathematical Games from Scientific American. New York: Scribner's, pp. 167-169, 1971.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, pp. 272-274, 1990.

Hall, J. F. "Fun with Stacking Blocks." Amer. J. Phys. 73, 1107-1116, 2005.

Havil, J. "Maximum Possible Overhang." §13.11 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 132-133, 2003.

Johnson, P. B. "Leaning Tower of Lire." Amer. J. Phys. 23, 240, 1955.

Paterson, M. and Zwick, U. "Overhang." In Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms, Held in Miami, FL, January 22-24, 2006 Philadelphia, PA: SIAM, pp. 231-240, 2006.

Pickover, C. A. "Some Experiments with a Leaning Tower of Books." Computer Language 7, 159-160, 1990.

Pickover, C. A. Computers and the Imagination. New York: St. Martin's Press, 1991.

Pickover, C. A. The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, p. 238, 2002.

Sharp, R. T. "Problem 52." Pi Mu Epsilon J. 1, 322, 1953.

Sharp, R. T. "Problem 52." Pi Mu Epsilon J. 2, 411, 1954.

Sloane, N. J. A. Sequences A001008/M2885, A002805/M1589, and A014537 in "The On-Line Encyclopedia of Integer Sequences."

Sutton, R. "A Problem of Balancing." Amer. J. Phys. 23, 547, 1955.

Walker, J. The Flying Circus of Physics with Answers. New York: Wiley, 1977.