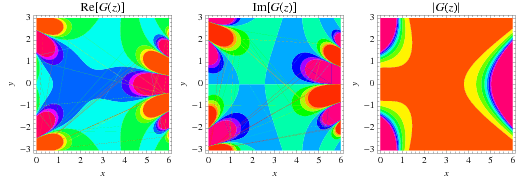
The Barnes 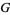-function is an analytic continuation of the 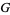-function defined in the construction of the Glaisher-Kinkelin constant

(1)

for 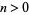, where  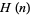is the hyperfactorial, which has the special values

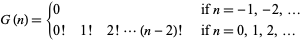(2)

for integer 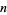. This function is what Sloane and Plouffe (1995) call the superfactorial, and the first few values for 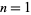, 2, ... are 1, 1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, ... (OEIS A000178).

The Barnes 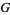-function can arise in spectral functions in mathematical physics (Voros 1987).

It is implemented in the Wolfram Language as BarnesG[n]. A special version of its natural logarithm optimized for large 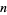 is implemented in the Wolfram Language as LogBarnesG[n].

The Barnes 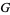-function for complex  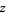may be defined by

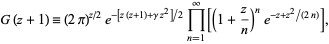(3)

where 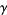 is the Euler-Mascheroni constant (Whittaker and Watson 1990, p. 264; Voros 1987). The product can be done in closed form, yielding the identity

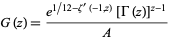(4)

for , where 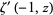 is the derivative of the Hurwitz zeta function,  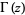is the gamma function, and  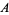is the Glaisher-Kinkelin constant. Another elegant closed-form expression is given by

(5)

where 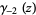 is a polygamma function of negative order. The Barnes 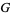-function and hyperfactorial  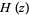satisfy the relation

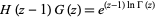(6)

for all complex 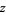, where  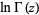is the log gamma function.

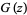 is an entire function analogous to 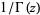, except that it has order 2 instead of 1.

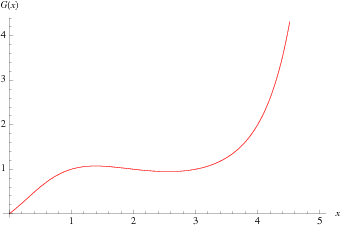
The Barnes 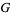-function is plotted above evaluated at integers values. A slight variant of the integer-valued Barnes 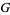-function is sometimes known as the superfactorial.

The Barnes 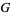-function satisfies the functional equation

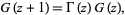(7)

and has the Taylor series

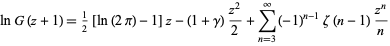(8)

in 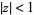. It also gives an analytic solution to the finite product

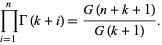(9)

The Barnes 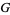-function has the equivalent reflection formulas

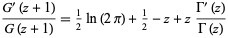(10)

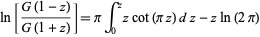(11)

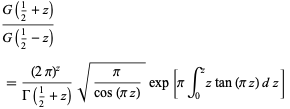(12)

(Voros 1987; Whittaker and Watson 1990, p. 264).

The derivative is given by

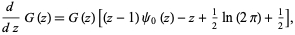(13)

where 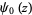 is the digamma function.

A Stirling-like asymptotic series for  as 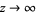 is given by

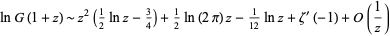(14)

(Voros 1987). This can be made more precise as

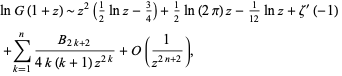(15)

where 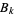 is a Bernoulli number (Adamchik 2001b; typo corrected).

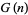 has the special values

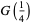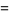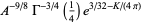			(16)
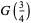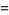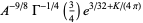			(17)
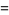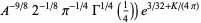			(18)

(OEIS A087013 and A087015) for 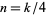, where  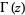is the gamma function,  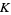is Catalan's constant,  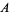is the Glaisher-Kinkelin constant, and

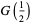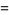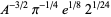			(19)
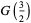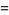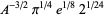			(20)
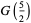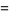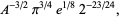			(21)

(OEIS A087014, A087016, and A087017) for 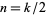, where  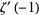is the derivative of the Riemann zeta function evaluated at 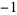. In general, for odd ,

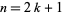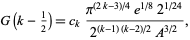(22)

where

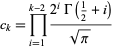(23)

for 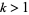, of which the first few terms are 1, 1, 1, 3, 45, 4725, 4465125, ... (OEIS A057863).

Another G-function is defined by Erdélyi et al. (1981, p. 20) as

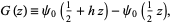(24)

where 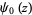 is the digamma function. An unrelated pair of functions are denote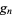d  and 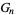 and are known as Ramanujan g- and G-functions.

REFERENCES:

Adamchik, V. "On the Barnes Function." Proceedings of the 2001 International Symposium on Symbolic and Algebraic Computation (July 22-25, 2001, London, Canada). New York: Academic Press, pp. 15-20, 2001a.

Adamchik, V. "Symbolic and Numeric Computation of the Barnes Functions." In Electronic Proceedings of the 7th International Conference on Applications of Computer Algebra. Albuquerque Technical Vocational Institute, Albuquerque, New Mexico, USA. May 31-June 3, 2001(Ed. M. Wester). 2001b. http://math.unm.edu/ACA/2001/Proceedings/SymNum/Adamchik_paper.pdf.

Barnes, E. W. "The Theory of the 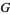-Function." Quart. J. Pure Appl. Math. 31, 264-314, 1900.

Dyson, F. J. "Fredholm Determinants and Inverse Scattering Problems." Commun. Math. Phys. 47, 171-183, 1976.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, 1981.

Glaisher, J. W. L. "On a Numerical Continued Product." Messenger Math. 6, 71-76, 1877.

Glaisher, J. W. L. "On the Product 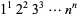." Messenger Math. 7, 43-47, 1878.

Glaisher, J. W. L. "On Certain Numerical Products." Messenger Math. 23, 145-175, 1893.

Glaisher, J. W. L. "On the Constant Which Occurs in the Formula for 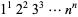." Messenger Math. 24, 1-16, 1894.

Kinkelin, H. "Über eine mit der Gammafunktion verwandte Transcendente und deren Anwendung auf die Integralrechnung." J. reine angew. Math. 57, 122-158, 1860.

Lenard, A. "Some Remarks on Large Toeplitz Matrices." Pacific J. Math. 42, 137-145, 1972.

McCoy, B. and Wu, T. T. The Two-Dimensional Ising Model. Cambridge, MA: Harvard University Press, p. 264 and Appendix B, 1973.

Mitra, S. and Nijenhuis, B. "Exact Conjectured Expressions for Correlations in the Dense 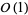 Loop Model on Cylinders." JSTAT, P10006, 2004.

Sloane, N. J. A. Sequences A000178/M2049, A057863, A087013, A087014, A087015, A087016, and A087017 in "The On-Line Encyclopedia of Integer Sequences."

Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Voros, A. "Spectral Functions, Special Functions and the Selberg Zeta Function." Commun. Math. Phys. 110, 439-465, 1987.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, p. 264, 1990.

Widom, H. "The Strong Szegö Limit Theorem for Circular Arcs." Indiana Univ. Math. J. 21, 277-283, 1971.

Widom, H. "Toeplitz Determinants with Singular Generating Functions." Amer. J. Math. 95, 333-383, 1973.