FLUX DENSITY VERSUS CURRENT

In a straight wire carrying a steady direct current surrounded by air or by free space (a vacuum), the flux density is greatest near the wire and diminishes with increasing distance from the wire. You ask, “Is there a formula that expresses flux density as a function of distance from the wire?” The answer is yes. Like all formulas in physics, it is perfectly accurate only under idealized circumstances.
Consider a wire that is perfectly thin, as well as perfectly straight. Suppose that it carries a current of I amperes. Let the flux density (in teslas) be denoted B. Consider a point P at a distance r (in meters) from the wire, as measured along the shortest possible route (that is, within a plane perpendicular to the wire). This is illustrated in Fig. 1. The following formula applies:
B = 2 × 10^-7 (I/r)
In this formula, the value 2 can be considered mathematically exact to any desired number of significant figures.
As long as the thickness of the wire is small compared with the distance r from it, and as long as the wire is reasonably straight in the vicinity of the point P at which the flux density is measured, this formula is a good indicator of what happens in real life.

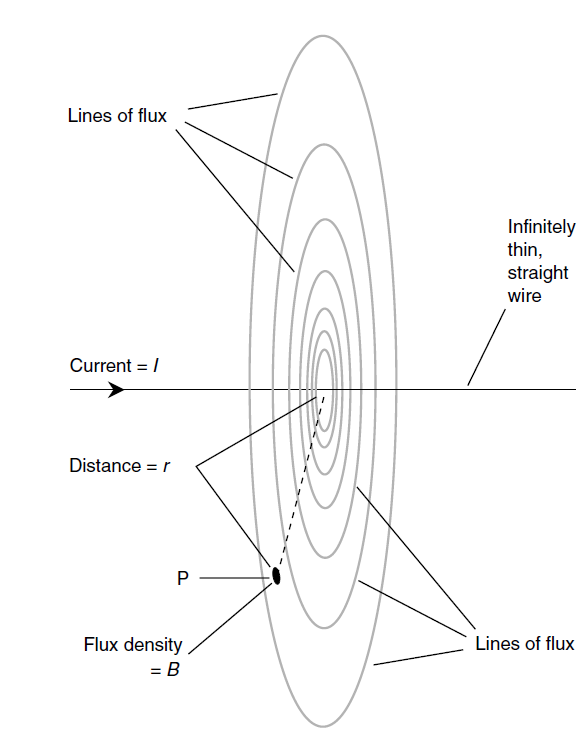
Fig. 1. Flux density varies inversely with the distance from a wire carrying direct current.

مواضيع ذات صلة

Thermal conductivity

Molecular diffusion

Ionic conductivity

The drift speed

Electrical transients

الشرر المقدس

الحقول الكهربية والشرر

الخلق غير المرئي

عجائب الكهرباء

مصادر الطاقة الكهربائية

التيارات الكهربائية التي تجري إلى الابد

النقل الكهربائي وقانون أوم