POINTS IN THE RC QUARTER-PLANE

Capacitive reactance can be plotted along a half-line or ray just as can inductive reactance. Capacitive and inductive reactance, considered as one, form a real-number line. The point where they join is the zeroreactance point.
In a circuit containing resistance and capacitive reactance, the characteristics are two-dimensional in a way that is analogous to the situation with the RL quarter-plane. The resistance ray and the capacitive-reactance ray can be placed end to end at right angles to make the RC quarter-plane (Fig. 1). Resistance is plotted horizontally, with increasing values toward the right. Capacitive reactance is plotted downward, with increasingly negative values as you go down.

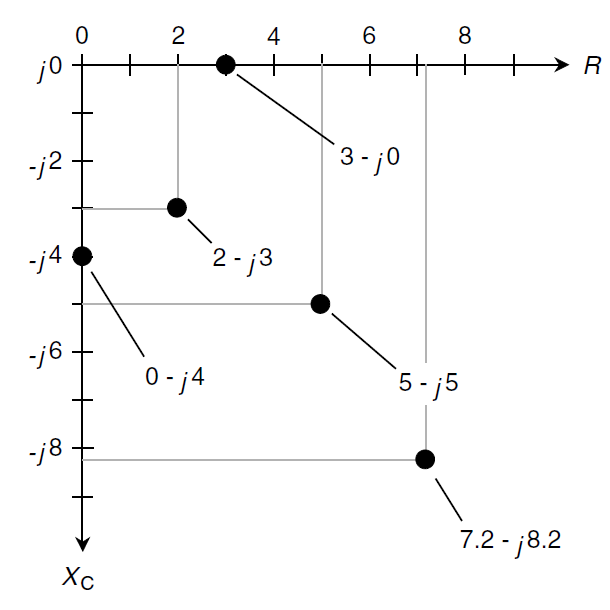
Fig. 1. The RC impedance quarter-plane showing five points for specific complex-number impedances.

Complex-number impedances that contain resistance and capacitance can be denoted in the form R+ jX_C; however, X_C is never positive. Because of this, scientists often write R - jX_C, dropping the minus sign from X_C and replacing addition with subtraction in the complex-number rendition.
If the resistance is pure, say, R = 3 ohms, then the complex-number impedance is 3 - j0, and this corresponds to the point (3, 0) on the RC quarter-plane. You might suspect that 3 - j0 is the same as 3 + j0 and that you need not even write the j0 part at all. In theory, both these notions are correct. However, writing the j0 part indicates that you are open to the possibility that there might be reactance in the circuit and that you’re working in two dimensions.
If you have a pure capacitive reactance, say, X_C = -4 ohms, then the complex-number impedance is 0 - j4, and this is at the point (0, -4) on the RC quarter-plane. Again, it’s important, for completeness, to write the 0 and not just the -j4. The points for 3 - j0 and 0 - j4, and three others, are plotted on the RC quarter-plane in Fig. 1.
In practical circuits, all capacitors have some leakage conductance. If the frequency goes to zero, that is, if the source is dc, a tiny current will flow because no dielectric is a perfect electrical insulator. Some capacitors have almost no leakage conductance, but none are completely free of it. Conversely, all electrical conductors have a little capacitive reactance simply because they occupy physical space. Thus there is no such thing as a mathematically pure conductor of ac either. The points 3 - j0 and 0 - j4 are idealized.
Remember that the values for X_C are reactances, not capacitances. Reactance varies with the frequency in an RC circuit. If you raise or lower the frequency, the value of X_C changes. A higher frequency causes X_C to get smaller negatively (closer to zero). A lower frequency causes X_C to get larger negatively (farther from zero or lower down on the RC quarter-plane). If the frequency goes to zero, then the capacitive reactance drops off the bottom of the plane, out of sight. In this case you have two plates or sets of plates having opposite electric charges but no “action.”

مواضيع ذات صلة

Thermal conductivity

Molecular diffusion

Ionic conductivity

The drift speed

Electrical transients

الشرر المقدس

الحقول الكهربية والشرر

الخلق غير المرئي

عجائب الكهرباء

مصادر الطاقة الكهربائية

التيارات الكهربائية التي تجري إلى الابد

النقل الكهربائي وقانون أوم