NEWTON’S SECOND LAW

We have seen that a force F acting on a mass m, produces an acceleration that 1) is in the direction of , and 2) has a magnitude inversely proportional to m. The simplest equation consistent with these observations is
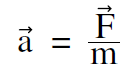.......(1)
Equation (1) turns out to be the correct relationship, and is known as Newton’s Second Law of Mechanics. (The First Law is a statement of the special case that, if there are no forces, there is no acceleration. That was not obvious in the late 1600s, and was therefore stated as a separate law.) A more familiar form of Newton’s second law, seen in all introductory physics texts is
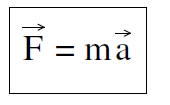........(1a)
If there is any equation that is essentially an icon for the introductory physics course, Equation (1a) is it.

At this point Equation (1) or (1a) serves more as a definition of force than a basic scientific result. We can, for example, see from Equation (1a) that force has the dimensions of mass times acceleration. In the MKS system of units this turns out to be kg(m/sec²), a collection of units called the newton. Thus we can say that we push on an object with a force of so many newtons. In the CGS system, the dimensions of force are gm(cm/sec²), a set of units called a dyne. A dyne turns out to be a very small unit of force, of the order of the force exerted by a fly doing push-ups. The newton is a much more convenient unit. The real confusion is in the English system of units where force is measured in pounds, and the unit of mass is a slug. We will carefully avoid doing Newton’s law calculations in English units so that the student does not have to worry about pounds and slugs.
At a more fundamental level, we can use Equation (1) to detect the existence of a force by the acceleration it produces. In projectile motion, how do we know that there is a gravitational force acting on the projectile?
Because of the gravitational acceleration. The acceleration  due to gravity is equal to 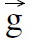(9.8 m/sec² directed downward), thus we can say that the gravitational force  that produces this acceleration is
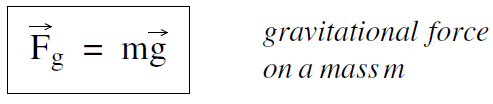....(2)
(2)
where m is the mass of the projectile.

Figure 1: The gravitational force between small masses is proportional to the product of the masses, and inversely proportional to the square of the separation between them.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل