Traveling Wave Formula

Thus far we have formulas for a time varying sine wave sin ωt , and a space varying wave sin kx. Now we want a formula for a traveling sine wave whose amplitude varies in both space and time. The answer turns out to be
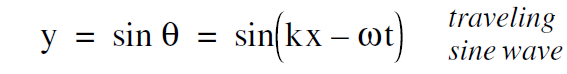..... (1)
What we will do is show that this formula represents a sine wave moving down the x axis. Figure (11) shows a sinusoidal shape that is moving down the x axis at a speed v_wave . If we describe the wave by the function sin θ , then it is the origin sin θ = 0 that moves down the axis at a speed v_wave . Thus what we need is a formula for θ so that when we set θ = 0 , that point does move down the x axis at the desired speed. The answer we gave in Equation 1 suggests that the correct formula for θ is

θ = kx – ωt (2)
Setting θ = 0 we get
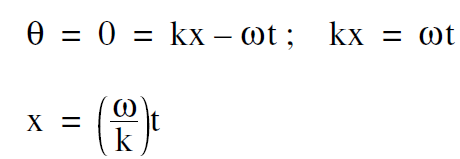 .....(3)
But if the θ = 0 point travels at a speed v_wave , then after a time t, it has traveled a distance x given by
x = v_wavet (4)

Comparing Equations (2) and (3), we see that the point θ = 0 moves along the x axis at a speed
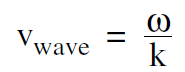(4)
You recognize that the quantity
ω/ k has the dimensions of a velocity
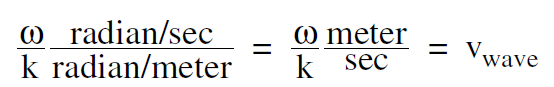...... (5)
Thus the origin does move down the x axis at a speed v_wave , and the formula (kx – ωt) , is our desired traveling wave formula.

Figure 1: The cycle begins at θ = 0.

مواضيع ذات صلة

أصول عدم الانعكاس

الانعكاس يولد الانعكاس

الاحتمالية في الميكانيكا الإحصائية

القابلية للانعكاس وعدم القابلية للانعكاس

نظرة في تعددية الفيزياء

الاختزال وعدم القابلية للانعكاس

الواقعية العلمية وتغيير النظريات

نقص الإثبات ومذهب الذرائعية ومذهب الواقعية

مشكلة التمييز: متى يكون المنهج علميا؟

المنهج العلمي: من الاستقراء إلى التكذيب وما بعده

مناهج العلوم وثمارها

!Parity is not conserved