Stability of Laser Resonators

For certain combinations of R₁, R₂, and L, the equations summarized in the previous subsection give nonphysical solutions (that is, imaginary spot sizes). This is the region where low-loss modes do not exist in the resonator.
Light rays that bounce back and forth between the spherical mirrors of a laser resonator experience a periodic focusing action. The effect on the rays is the same as in a periodic sequence of lenses. Rays passing through a stable sequence of lenses are periodically refocused. For unstable systems the rays become more and more dispersed the further they pass through the sequence. In an optical resonator operated in the stable region, the waves propagate between reflectors without spreading appreciably. This fact can be expressed by a stability criterion
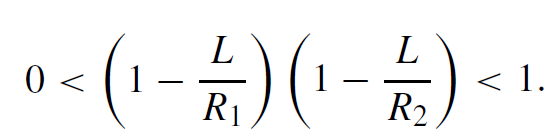.......(1)

To show graphically which type of resonator is stable and which is unstable, it is useful to plot a stability diagram in which each particular resonator geometry is represented by a point. This is shown in Fig. 1, where the parameters

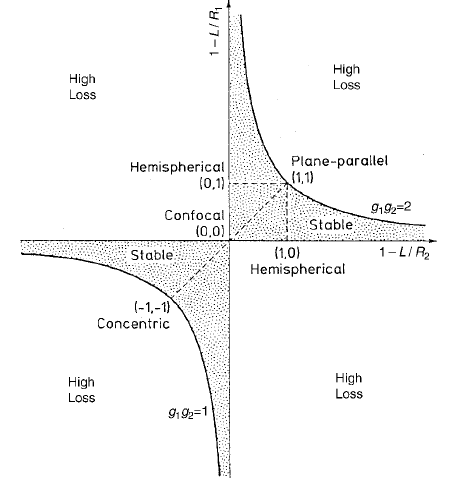
FIGURE 1. Stability diagram for the passive laser resonator.

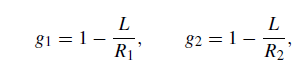...........(2)

are drawn as the coordinate axes.
All cavity configurations are unstable unless they correspond to points located in the area enclosed by a branch of the hyperbola g₁g₂ = 1 and the coordinate axes. The origin of the diagram represents the confocal system.
The resonators located along the dashed line, oriented at 45^◦ with respect to the coordinate axis, are symmetric configurations, that is, they have mirrors with the same radius of curvature.
The diagram is divided into positive and negative branches defining quadrants for which g₁g₂ is either positive or negative. The reason for this classification becomes clear when we discuss unstable resonators.

مواضيع ذات صلة

الليزرات والسوائل التي تصعد إلى الأعلى

الليزر والميزر

Flashtube Explosion

Tube Failure

Plane–Parallel Resonator

Concave–Convex Resonator

Plano-Concave Resonator

Mirrors of Equal Curvature

Parasitic Oscillations

Prelasing

Depopulation Losses

The Three-Level System