

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Kurtosis
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
20-2-2021
2810
Kurtosis is defined as a normalized form of the fourth central moment 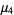 of a distribution. There are several flavors of kurtosis, the most commonly encountered variety of which is normally termed simply "the" kurtosis and is denoted
of a distribution. There are several flavors of kurtosis, the most commonly encountered variety of which is normally termed simply "the" kurtosis and is denoted 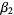 (Pearson's notation; Abramowitz and Stegun 1972, p. 928) or
(Pearson's notation; Abramowitz and Stegun 1972, p. 928) or 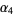 (Kenney and Keeping 1951, p. 27; Kenney and Keeping 1961, pp. 99-102). The kurtosis of a theoretical distribution is defined by
(Kenney and Keeping 1951, p. 27; Kenney and Keeping 1961, pp. 99-102). The kurtosis of a theoretical distribution is defined by
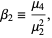 |
(1) |
where 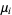 denotes the
denotes the 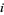 th central moment (and in particular,
th central moment (and in particular, 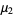 is the variance). This form is implemented in the Wolfram Language as Kurtosis[dist].
is the variance). This form is implemented in the Wolfram Language as Kurtosis[dist].
The "kurtosis excess" (Kenney and Keeping 1951, p. 27) is defined by
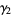 |
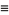 |
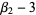 |
(2) |
 |
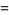 |
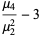 |
(3) |
and is commonly denoted 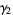 (Abramowitz and Stegun 1972, p. 928) or
(Abramowitz and Stegun 1972, p. 928) or 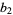 . Kurtosis excess is commonly used because
. Kurtosis excess is commonly used because 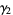 of a normal distribution is equal to 0, while the kurtosis proper is equal to 3. Unfortunately, Abramowitz and Stegun (1972) confusingly refer to
of a normal distribution is equal to 0, while the kurtosis proper is equal to 3. Unfortunately, Abramowitz and Stegun (1972) confusingly refer to 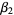 as the "excess or kurtosis."
as the "excess or kurtosis."
For many distributions encountered in practice, a positive 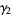 corresponds to a sharper peak with higher tails than if the distribution were normal (Kenney and Keeping 1951, p. 54). This observation is likely the reason kurtosis excess was historically (but incorrectly) regarded as a measure of the "peakedness" of a distribution. However, the correspondence between kurtosis and peakedness is not true in general; in fact, a distribution with a perfectly flat top may have infinite kurtosis, while one with infinite peakedness may have negative kurtosis excess. As a result, kurtosis excess provides a measure of outliers (i.e., the presence of "heavy tails") in a distribution, not its degree of peakedness (Kaplansky 1945; Kenney and Keeping 1951, p. 27; Westfall 2014).
corresponds to a sharper peak with higher tails than if the distribution were normal (Kenney and Keeping 1951, p. 54). This observation is likely the reason kurtosis excess was historically (but incorrectly) regarded as a measure of the "peakedness" of a distribution. However, the correspondence between kurtosis and peakedness is not true in general; in fact, a distribution with a perfectly flat top may have infinite kurtosis, while one with infinite peakedness may have negative kurtosis excess. As a result, kurtosis excess provides a measure of outliers (i.e., the presence of "heavy tails") in a distribution, not its degree of peakedness (Kaplansky 1945; Kenney and Keeping 1951, p. 27; Westfall 2014).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 928, 1972.
Darlington, R. B. "Is Kurtosis Really Peakedness?" Amer. Statist. 24, 19-22, 1970.
Dodge, Y. and Rousson, V. "The Complications of the Fourth Central Moment." Amer. Statist. 53, 267-269, 1999.
Kaplansky, I. "A Common Error Concerning Kurtosis." J. Amer. Stat. Assoc. 40, 259, 1945.
Kenney, J. F. and Keeping, E. S. "Kurtosis." §7.12 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 102-103, 1962.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Moors, J. J. A. "The Meaning of Kurtosis: Darlington Reexamined." Amer. Statist. 40, 283-284, 1986.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Moments of a Distribution: Mean, Variance, Skewness, and So Forth." §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.
Ruppert, D. "What is Kurtosis? An Influence Function Approach." Amer. Statist. 41, 1-5, 1987.
Westfall, P. H. "Kurtosis as Peakedness, 1905-2014. R.I.P." Amer. Statist. 68, 191-195, 2014.