

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Mean Deviation
المؤلف:
Kenney, J. F. and Keeping, E. S.
المصدر:
"Mean Absolute Deviation." §6.4 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand
الجزء والصفحة:
...
20-2-2021
1687
The mean deviation (also called the mean absolute deviation) is the mean of the absolute deviations of a set of data about the data's mean. For a sample size 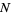 , the mean deviation is defined by
, the mean deviation is defined by
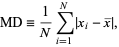 |
(1) |
where  is the mean of the distribution. The mean deviation of a list of numbers is implemented in the Wolfram Language as MeanDeviation[data].
is the mean of the distribution. The mean deviation of a list of numbers is implemented in the Wolfram Language as MeanDeviation[data].
The mean deviation for a discrete distribution 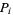 defined for
defined for 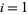 , 2, ...,
, 2, ..., 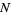 is given by
is given by
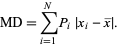 |
(2) |
Mean deviation is an important descriptive statistic that is not frequently encountered in mathematical statistics. This is essentially because while mean deviation has a natural intuitive definition as the "mean deviation from the mean," the introduction of the absolute value makes analytical calculations using this statistic much more complicated than the standard deviation
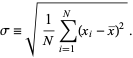 |
(3) |
As a result, least squares fitting and other standard statistical techniques rely on minimizing the sum of square residuals instead of the sum of absolute residuals.
For example, consider the discrete uniform distribution consisting of 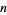 possible outcomes with
possible outcomes with 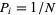 for
for 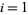 , 2, ...,
, 2, ..., 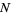 . The mean is given by
. The mean is given by
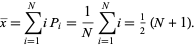 |
(4) |
The variance (and therefore its square root, namely the standard deviation) is also straightforward to obtain as
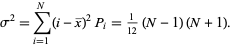 |
(5) |
On the other hand, the mean deviation is given by
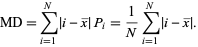 |
(6) |
This can be obtained in closed form, but is much more unwieldy since it requires breaking up the summand into two pieces and treating the cases of 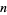 even and odd separately.
even and odd separately.
The following table summarizes the mean absolute deviations for some named continuous distributions, where 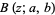 is an incomplete beta function,
is an incomplete beta function, 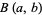 is a beta function,
is a beta function, 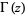 is a gamma function,
is a gamma function, 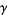 is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 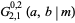 is a Meijer G-function,
is a Meijer G-function, 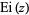 is the exponential integral function,
is the exponential integral function, 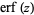 is erf, and
is erf, and 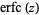 is erfc.
is erfc.
| distribution | M.D. |
| beta distribution | 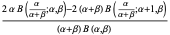 |
| chi-squared distribution | 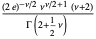 |
| exponential distribution | 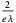 |
| gamma distribution | 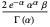 |
| Gumbel distribution | ![beta[G_(2,1)^(2,0)(e,gamma^(-1)|1,1; 0)-Ei(sinhgamma-coshgamma)]](https://mathworld.wolfram.com/images/equations/MeanDeviation/Inline23.gif) |
| half-normal distribution | ![2/theta[e^(-1/pi)+erf(1/(sqrt(pi)))]](https://mathworld.wolfram.com/images/equations/MeanDeviation/Inline24.gif) |
| Laplace distribution | 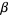 |
| logistic distribution | 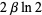 |
| log normal distribution | 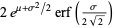 |
| Maxwell distribution | ![4e^(-4/pi)sqrt(2/pi)sigma[1+e^(4/pi)erf(2/(sqrt(pi)))]](https://mathworld.wolfram.com/images/equations/MeanDeviation/Inline28.gif) |
| normal distribution | 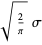 |
| Pareto distribution | 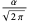 |
| Rayleigh distribution | 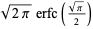 |
| Student's t-distribution | 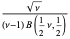 |
| Student's t-distribution | 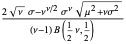 |
| triangular distribution | 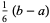 |
| triangular distribution | |
| uniform distribution | 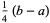 |
The following table summarizes the mean absolute deviations for some named discrete distributions, where 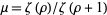 .
.
| distribution | M.D. |
| Bernoulli distribution | 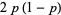 |
| binomial distribution | 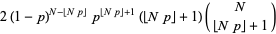 |
| discrete uniform distribution | |
| geometric distribution | 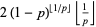 |
| Poisson distribution | 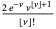 |
| Zipf distribution | ![(2[zeta(rho+1)zeta(rho,|_mu_|+1)-zeta(rho)zeta(rho+1,|_mu_|+1)])/(zeta^2(rho+1))](https://mathworld.wolfram.com/images/equations/MeanDeviation/Inline43.gif) |
REFERENCES:
Havil, J. "Ways of Means." §13.1 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 119-121, 2003.
Kenney, J. F. and Keeping, E. S. "Mean Absolute Deviation." §6.4 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 76-77 1962.