

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Saint Petersburg Paradox
المؤلف:
Ball, W. W. R. and Coxeter, H. S. M.
المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover
الجزء والصفحة:
...
15-3-2021
2757
Consider a game, first proposed by Nicolaus Bernoulli, in which a player bets on how many tosses of a coin will be needed before it first turns up heads. The player pays a fixed amount initially, and then receives 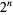 dollars if the coin comes up heads on the
dollars if the coin comes up heads on the 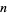 th toss. The expectation value of the gain is then
th toss. The expectation value of the gain is then
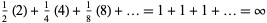 |
(1) |
dollars, so any finite amount of money can be wagered and the player will still come out ahead on average.
Feller (1968) discusses a modified version of the game in which the player receives nothing if a trial takes more than a fixed number 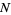 of tosses. The classical theory of this modified game concluded that
of tosses. The classical theory of this modified game concluded that 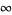 is a fair entrance fee, but Feller notes that "the modern student will hardly understand the mysterious discussions of this 'paradox.' "
is a fair entrance fee, but Feller notes that "the modern student will hardly understand the mysterious discussions of this 'paradox.' "
In another modified version of the game, the player bets $2 that heads will turn up on the first throw, $4 that heads will turn up on the second throw (if it did not turn up on the first), $8 that heads will turn up on the third throw, etc. Then the expected payoff is
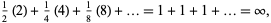 |
(2) |
so the player can apparently be in the hole by any amount of money and still come out ahead in the end. This paradox can clearly be resolved by making the distinction between the amount of the final payoff and the net amount won in the game. It is misleading to consider the payoff without taking into account the amount lost on previous bets, as can be shown as follows. At the time the player first wins (say, on the 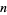 th toss), he will have lost
th toss), he will have lost
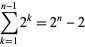 |
(3) |
dollars. In this toss, however, he wins 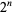 dollars. This means that the net gain for the player is a whopping $2, no matter how many tosses it takes to finally win. As expected, the large payoff after a long run of tails is exactly balanced by the large amount that the player has to invest. In fact, by noting that the probability of winning on the
dollars. This means that the net gain for the player is a whopping $2, no matter how many tosses it takes to finally win. As expected, the large payoff after a long run of tails is exactly balanced by the large amount that the player has to invest. In fact, by noting that the probability of winning on the 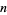 th toss is
th toss is 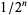 , it can be seen that the probability distribution for the number of tosses needed to win is simply a geometric distribution with
, it can be seen that the probability distribution for the number of tosses needed to win is simply a geometric distribution with 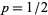 .
.
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 201-202, 1987.
Erickson, G. W. and Fossa, J. A. Dictionary of Paradox. Lanham, MD: University Press of America, pp. 13-15, 1998.
Eves, H. An Introduction to the History of Mathematics, 3rd ed. New York: Holt, Rinehart and Winston, p. 343, 1969.
Feller, W. "The Petersburg Game." §10.4 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 235-237, 1968.
Gardner, M. Hexaflexagons and Other Mathematical Diversions: The First Scientific American Book of Puzzles and Games. New York: Simon and Schuster, pp. 51-52, 1959.
Kamke, E. Einführung in die Wahrscheinlichkeitstheorie. Leipzig, Germany, pp. 82-89, 1932.
Keynes, J. M. K. "The Application of Probability to Conduct." Part VII, Ch. 4 in The World of Mathematics, Vol. 2 (Ed. K. Newman). New York: Dover, pp. 1360-1379, 2000.
Kraitchik, M. "The Saint Petersburg Paradox." §6.18 in Mathematical Recreations. New York: W. W. Norton, pp. 138-139, 1942.
Todhunter, I. §391 in History of the Mathematical Theory of Probability. New York: Chelsea, p. 221, 1949.