

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Distribution Function
المؤلف:
Abramowitz, M. and Stegun, I. A. (Eds.)
المصدر:
"Probability Functions." Ch. 26 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
19-4-2021
1625
The distribution function 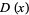 , also called the cumulative distribution function (CDF) or cumulative frequency function, describes the probability that a variate
, also called the cumulative distribution function (CDF) or cumulative frequency function, describes the probability that a variate 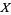 takes on a value less than or equal to a number
takes on a value less than or equal to a number  . The distribution function is sometimes also denoted
. The distribution function is sometimes also denoted 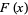 (Evans et al. 2000, p. 6).
(Evans et al. 2000, p. 6).
The distribution function is therefore related to a continuous probability density function 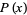 by
by
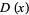 |
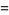 |
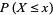 |
(1) |
 |
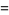 |
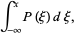 |
(2) |
so 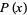 (when it exists) is simply the derivative of the distribution function
(when it exists) is simply the derivative of the distribution function
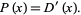 |
(3) |
Similarly, the distribution function is related to a discrete probability 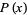 by
by
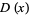 |
 |
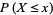 |
(4) |
 |
 |
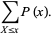 |
(5) |
There exist distributions that are neither continuous nor discrete.
A joint distribution function can be defined if outcomes are dependent on two parameters:
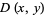 |
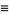 |
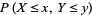 |
(6) |
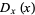 |
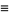 |
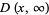 |
(7) |
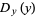 |
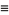 |
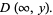 |
(8) |
Similarly, a multivariate distribution function can be defined if outcomes depend on 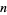 parameters:
parameters:
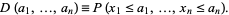 |
(9) |
The probability content of a closed region can be found much more efficiently than by direct integration of the probability density function 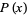 by appropriate evaluation of the distribution function at all possible extrema defined on the region (Rose and Smith 1996; 2002, p. 193). For example, for a bivariate distribution function
by appropriate evaluation of the distribution function at all possible extrema defined on the region (Rose and Smith 1996; 2002, p. 193). For example, for a bivariate distribution function 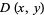 , the probability content in the region
, the probability content in the region 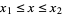 ,
, 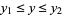 is given by
is given by
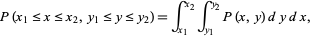 |
(10) |
but can be computed much more efficiently using
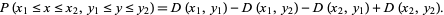 |
(11) |
Given a continuous 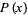 , assume you wish to generate numbers distributed as
, assume you wish to generate numbers distributed as 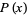 using a random number generator. If the random number generator yields a uniformly distributed value
using a random number generator. If the random number generator yields a uniformly distributed value 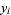 in
in ![[0,1]](https://mathworld.wolfram.com/images/equations/DistributionFunction/Inline37.gif) for each trial
for each trial 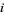 , then compute
, then compute
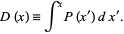 |
(12) |
The formula connecting 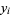 with a variable distributed as
with a variable distributed as 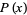 is then
is then
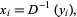 |
(13) |
where 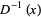 is the inverse function of
is the inverse function of 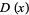 . For example, if
. For example, if 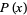 were a normal distribution so that
were a normal distribution so that
![D(x)=1/2[1+erf((x-mu)/(sigmasqrt(2)))],](https://mathworld.wolfram.com/images/equations/DistributionFunction/NumberedEquation7.gif) |
(14) |
then
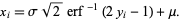 |
(15) |
A distribution with constant variance of 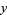 for all values of
for all values of  is known as a homoscedastic distribution. The method of finding the value at which the distribution is a maximum is known as the maximum likelihood method.
is known as a homoscedastic distribution. The method of finding the value at which the distribution is a maximum is known as the maximum likelihood method.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Probability Functions." Ch. 26 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 925-964, 1972.
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, pp. 6-8, 2000.
Iyanaga, S. and Kawada, Y. (Eds.). "Distribution of Typical Random Variables." Appendix A, Table 22 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1483-1486, 1980.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 92-94, 1984.
Rose, C. and Smith, M. D. "The Multivariate Normal Distribution." Mathematica J. 6, 32-37, 1996.
Rose, C. and Smith, M. D. Mathematical Statistics with Mathematica. New York: Springer-Verlag, 2002.