There are no fewer than two closely related but somewhat different notions of gerbe in mathematics.

For a fixed topological space 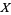, a gerbe on  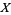can refer to a stack of groupoids  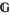on 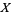 satisfying the properties

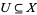1.  for subsets  open, and

2. given objects 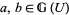, any point  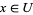has a neighborhood  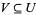for which there is at least one morphism  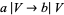in .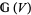

The second definition is due to Giraud (Brylinski 1993). Given a manifold 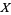 and a Lie group 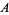, a gerbe  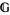with band  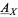is a sheaf of groupoids over  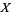satisfying the following three properties:

1. Given any object 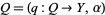 of 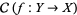, the sheaf  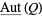of automorphisms of this object is a sheaf of groups on  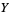which is locally isomorphic to the sheaf  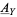of smooth 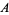-valued functions. Such a local isomorphism  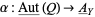is unique up to inner automorphisms of .

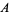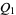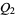2. Given two objects  and  of 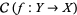, there exists a surjective local homeomorphism  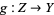such that  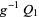and 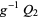 are isomorphic. In particular,  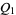and 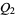 are locally isomorphic.

3. There exists a surjective local homeomorphism 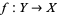 such that the category  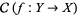is non-empty.

Clearly, the notion of a gerbe's band is fundamental for the second definition; though not explicitly mentioned, the band of a gerbe 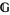 defined by the first definition is also important (Moerdijk 2002). According to Brylinski, gerbes whose bands  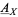corresponds to a Lie group  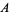are significant in that they give rise to degree-2 cohomology classes in 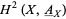, a fact utilized by Giraud in his study of non-abelian degree-2 cohomology.

REFERENCES:

Brylinski, J. Loop Spaces, Characteristic Classes and Geometric Quantization. Boston, MA: Birkhäuser, 1993.

Moerdijk, I. "Introduction to the Language of Stacks and Gerbes." 2002. https://arxiv.org/abs/math/0212266.