

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Additive Cellular Automaton
المؤلف:
Wolfram, S
المصدر:
A New Kind of Science. Champaign, IL: Wolfram Media
الجزء والصفحة:
pp. 264, 870, and 952-953
21-8-2021
1511
An additive cellular automaton is a cellular automaton whose rule is compatible with an addition of states. Typically, this addition is derived from modular arithmetic. Additive rules allow the evolution for different initial conditions to be computed independently, then the results combined by simply adding. The results for arbitrary starting conditions can therefore be computed very efficiently by convolving the evolution of a single cell with an appropriate convolution kernel (which, in the case of two-color automata, would correspond to the set of initially "active" cells).

A simple example of an additive cellular automaton is provided by the rule 90 elementary cellular automaton. As can be seen from the graphical representation of this rule, the rule as a function of left, central, and right neighbors is simply given by the sum of the rules for the left and right neighbors taken modulo 2, where white cells are assigned the value 0 and black cells are assigned 1. (This is equivalent to the XOR operation and means that "adding" two white cells or two black cells gives a white cell, while adding one white and one black cells gives a black cell.) For example, the rule for (1, 1, 1) is 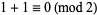 , the rule for (1, 1, 0) is
, the rule for (1, 1, 0) is 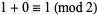 , the rule for (1, 0, 1) is
, the rule for (1, 0, 1) is 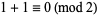 , and so on. Repeating this for each of the
, and so on. Repeating this for each of the 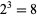 possible states of neighbors gives
possible states of neighbors gives
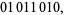 |
(1) |
which is exactly the binary string defining the behavior of rule 90 (this rule is assigned the number 90 is because 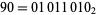 in binary).
in binary).

The evolution of shifted versions of rule 90 are illustrated in the above figure. The figure on the left shows 31 iterations of rule 90 for an initial condition consisting of a single black square. Moving to the right, each figure shows the results of adding an additional black cell with displacement 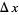 to the starting condition, increasing one generation per frame.
to the starting condition, increasing one generation per frame.

The illustration above shows the additivity more explicitly. In this animation, each frame corresponds to an initial conditions with the right cell shifted one unit further to the right. As can be seen, the portion of the pattern that does not overlap remains unchanged, while the overlapping portion is additive under the XOR operation.
In general, a cellular automaton with 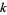 colors is additive if its rules can be written as a sum of integer multiples of its neighbors (mod
colors is additive if its rules can be written as a sum of integer multiples of its neighbors (mod 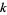 ), where the integers can range from 0 to
), where the integers can range from 0 to 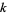 . There are therefore
. There are therefore 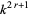 additive rules among the
additive rules among the 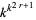 possible rules with
possible rules with 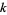 colors and range
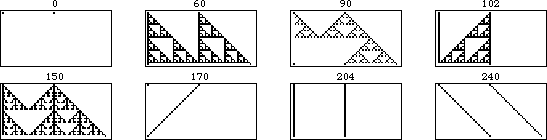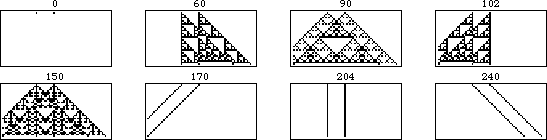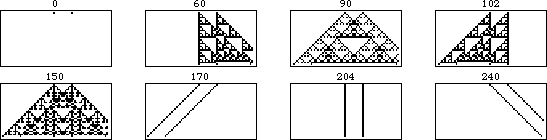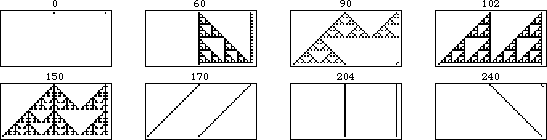
colors and range 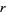 (Wolfram 2002, p. 952). The table below summarize the eight additive rules for the elementary cellular automata (
(Wolfram 2002, p. 952). The table below summarize the eight additive rules for the elementary cellular automata (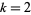 and
and 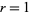 gives
gives 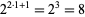 ). In the table,
). In the table, 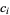 denotes the neighbor located at position
denotes the neighbor located at position 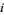 relative to the center.
relative to the center.
| rule | addition (mod 2) |
| 0 | 0 |
| rule 60 | 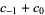 |
| rule 90 | 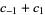 |
| rule 102 | 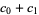 |
| rule 150 | 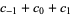 |
| 170 | 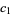 |
| 204 | 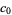 |
| 240 | 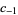 |
For additivity of the above automata, the properties required were associativity and commutativity. It is possible to generalize the notion of additivity to other types of addition. In general, let 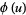 denote the cellular automaton evolution history of
denote the cellular automaton evolution history of 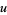 , and let
, and let 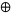 denote a binary operator acting on the values of cells and, by extension, to their states and evolution. Then
denote a binary operator acting on the values of cells and, by extension, to their states and evolution. Then 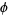 is an additive cellular automaton with respect to
is an additive cellular automaton with respect to 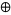 if
if
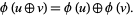 |
(2) |
Some cellular automata have no interesting 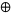 , but others do, and these additions can be used to speed up calculations.
, but others do, and these additions can be used to speed up calculations.

Rule 250 provides another example of an additive elementary cellular automaton under the operation OR(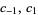 ). By examining the set of rules, it can be verified that in each case, the resultant state is black if either (or both) neighbors is black, and white only if both neighbors are white. This corresponds to the set of rules
). By examining the set of rules, it can be verified that in each case, the resultant state is black if either (or both) neighbors is black, and white only if both neighbors are white. This corresponds to the set of rules
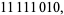 |
(3) |
which is identical to the definition of rule 250.


Generation-by-generation differences for the first few shifts and the entire pattern as a function of shift are illustrated above.
As a result of additivity, the evolutions of additive cellular automata behave similarly to the solutions of linear partial differential equations. In particular, they admit analogs of Green's functions such that, given an initial condition, the resulting evolution can be found by convolving the evolution of a single cell (which can be viewed as the analog of an integral kernel) with the initial condition (Wolfram 2002, p. 952).
REFERENCES:
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 264, 870, and 952-953, 2002.