

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Newton,s Method
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
24-9-2021
1320
Newton's method, also called the Newton-Raphson method, is a root-finding algorithm that uses the first few terms of the Taylor series of a function  in the vicinity of a suspected root. Newton's method is sometimes also known as Newton's iteration, although in this work the latter term is reserved to the application of Newton's method for computing square roots.
in the vicinity of a suspected root. Newton's method is sometimes also known as Newton's iteration, although in this work the latter term is reserved to the application of Newton's method for computing square roots.
For  a polynomial, Newton's method is essentially the same as Horner's method.
a polynomial, Newton's method is essentially the same as Horner's method.
The Taylor series of  about the point
about the point  is given by
is given by
 |
(1) |
Keeping terms only to first order,
 |
(2) |
Equation (2) is the equation of the tangent line to the curve at  , so
, so  is the place where that tangent line intersects the
is the place where that tangent line intersects the  -axis. A graph can therefore give a good intuitive idea of why Newton's method works at a well-chosen starting point and why it might diverge with a poorly-chosen starting point.
-axis. A graph can therefore give a good intuitive idea of why Newton's method works at a well-chosen starting point and why it might diverge with a poorly-chosen starting point.
This expression above can be used to estimate the amount of offset  needed to land closer to the root starting from an initial guess
needed to land closer to the root starting from an initial guess  . Setting
. Setting  and solving (2) for
and solving (2) for  gives
gives
 |
(3) |
which is the first-order adjustment to the root's position. By letting  , calculating a new
, calculating a new  , and so on, the process can be repeated until it converges to a fixed point (which is precisely a root) using
, and so on, the process can be repeated until it converges to a fixed point (which is precisely a root) using
 |
(4) |
Unfortunately, this procedure can be unstable near a horizontal asymptote or a local extremum. However, with a good initial choice of the root's position, the algorithm can be applied iteratively to obtain
 |
(5) |
for  , 2, 3, .... An initial point
, 2, 3, .... An initial point  that provides safe convergence of Newton's method is called an approximate zero.
that provides safe convergence of Newton's method is called an approximate zero.
Newton's method can be implemented in the Wolfram Language as
NewtonsMethodList[f_, {x_, x0_}, n_] :=
NestList[# - Function[x, f][#]/
Derivative[1][Function[x, f]][#]& , x0, n]
Assume that Newton's iteration  converges toward
converges toward  with
with  , and define the error after the
, and define the error after the  th step by
th step by
 |
(6) |
Expanding  about
about  gives
gives
 |
 |
 |
(7) |
 |
 |
 |
(8) |
 |
 |
 |
(9) |
But
 |
 |
 |
(10) |
 |
 |
 |
(11) |
 |
 |
 |
(12) |
Taking the second-order expansion
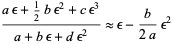 |
(13) |
gives
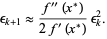 |
(14) |
Therefore, when the method converges, it does so quadratically.

Applying Newton's method to the roots of any polynomial of degree two or higher yields a rational map of  , and the Julia set of this map is a fractal whenever there are three or more distinct roots. Iterating the method for the roots of
, and the Julia set of this map is a fractal whenever there are three or more distinct roots. Iterating the method for the roots of  with starting point
with starting point  gives
gives
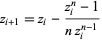 |
(15) |
(Mandelbrot 1983, Gleick 1988, Peitgen and Saupe 1988, Press et al. 1992, Dickau 1997). Since this is an  th order polynomial, there are
th order polynomial, there are  roots to which the algorithm can converge. Coloring the basin of attraction (the set of initial points
roots to which the algorithm can converge. Coloring the basin of attraction (the set of initial points  that converge to the same root) for each root a different color then gives the above plots.
that converge to the same root) for each root a different color then gives the above plots.

Fractals typically arise from non-polynomial maps as well. The plot above shows the number of iterations needed for Newton's method to converge for the function  (D. Cross, pers. comm., Jan. 10, 2005) and
(D. Cross, pers. comm., Jan. 10, 2005) and  .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 18, 1972.
Acton, F. S. Ch. 2 in Numerical Methods That Work. Washington, DC: Math. Assoc. Amer., 1990.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 963-964, 1985.
Boyer, C. B. and Merzbacher, U. C. A History of Mathematics, 2nd ed. New York: Wiley, 1991.
Dickau, R. M. "Basins of Attraction for 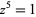 Using Newton's Method in the Complex Plane." http://mathforum.org/advanced/robertd/newtons.html.
Using Newton's Method in the Complex Plane." http://mathforum.org/advanced/robertd/newtons.html.
Dickau, R. M. "Variations on Newton's Method." http://mathforum.org/advanced/robertd/newnewton.html.
Dickau, R. M. "Compilation of Iterative and List Operations." Mathematica J. 7, 14-15, 1997.
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, plate 6 (following p. 114) and p. 220, 1988.
Gourdon, X. and Sebah, P. "Newton's Iteration." http://numbers.computation.free.fr/Constants/Algorithms/newton.html.
Householder, A. S. Principles of Numerical Analysis. New York: McGraw-Hill, pp. 135-138, 1953.
Mandelbrot, B. B. The Fractal Geometry of Nature. San Francisco, CA: W. H. Freeman, 1983.
Newton, I. Methodus fluxionum et serierum infinitarum. 1664-1671.
Ortega, J. M. and Rheinboldt, W. C. Iterative Solution of Nonlinear Equations in Several Variables. Philadelphia, PA: SIAM, 2000.
Peitgen, H.-O. and Saupe, D. The Science of Fractal Images. New York: Springer-Verlag, 1988.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Newton-Raphson Method Using Derivatives" and "Newton-Raphson Methods for Nonlinear Systems of Equations." §9.4 and 9.6 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 355-362 and 372-375, 1992.
Ralston, A. and Rabinowitz, P. §8.4 in A First Course in Numerical Analysis, 2nd ed. New York: McGraw-Hill, 1978.
Raphson, J. Analysis aequationum universalis. London, 1690.
Smale, S. "On the Efficiency of Algorithms of Analysis." Bull. Amer. Math. Soc. 13, 87-121, 1985.
Varona, J. L. "Graphic and Numerical Comparison Between Iterative Methods." Math. Intell. 24, 37-46, 2002.
Whittaker, E. T. and Robinson, G. "The Newton-Raphson Method." §44 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 84-87, 1967.