Birkhoff,s Inequality
المؤلف:
Jentzsch, R
المصدر:
"Über Integralgleichungen mit positivem Kern." J. reine angew. Math. 141
الجزء والصفحة:
...
6-10-2021
1343
Birkhoff's Inequality
In homogeneous coordinates, the first positive quadrant joins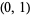 
with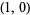 
by "points" 
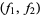, and is mapped onto the hyperbolic line 
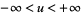by the correspondence 
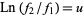. Now define
 |
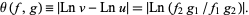(1)
|
Let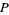 
be any bounded linear transformation of a Banach space 
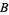that maps a closed convex cone 
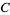of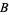 
onto itself. Then the 
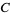-norm 
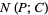of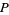 
is defined by
 |
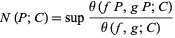(2)
|
for pairs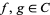 
with finite 
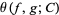. Birkhoff's inequality then states that if the transform 
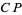of 
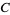under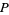 
has finite diameter 
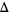under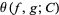 
, then
 |
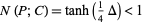(3)
|
(Birkhoff 1957).
REFERENCES:
Birkhoff, G. "Extensions of Jentzsch's Theorem." Trans. Amer. Math. Soc. 85, 219-227, 1957.
Jentzsch, R. "Über Integralgleichungen mit positivem Kern." J. reine angew. Math. 141, 235-244, 1912.
Schmeidler, W. Integralgleichungen mit Anwendungen in Physik und Technik, Vol. 1. Lineare Integralgleichungen. Leipzig, Germany: Geest & Portig, p. 298, 1955.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
