الدالة الفردية :  Odd Function

هي الدالة التي تحقق لكل قيم المتغير في المجال الخاصية :

                                      F(-x) = - f(x)

وتسمى الدالة التي لها هذه الخاصية بالدالة الفردية .

مثال : لدينا الدالة :

                                      F(x) = x³

مثل الاقتران بيانياً.

الحل:

نمثل الاقتران بيانياً على المستوى الديكارتي بتكوين جدول لبعض قيم (y) المناظرة.

ثم نقوم بتعيين النقاط في الجدول السابق على المستوى الديكارتي ، ونرسم منحنى الدالة ـ، وتسمى الدالة التي لها هذه الصيغة بالدالة الفردية. انظر إلى الشكل التالي.

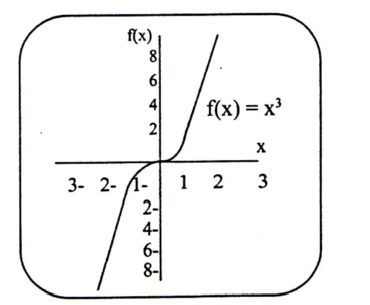
شكل (1-2)

منحنى الدالة الفردية يكون متماثلاً حول نقطة الأصل والعكس صحيح ، بمعنى ، أن كل دالة متماثل حول نقطة الأصل يكون فردياً.

ملاحظة مهمة : ليس بالضرورة أن تكون الدالة زوجية أو فردية ، حيث إن الكثير من الدوال ليست زوجية وليست فردية.

ملاحظة : بعدما مثلنا هذه الدوال الواردة في الأمثلة والتي هي كلها من عائلة كثيرات الحدود ، ننتقل الآن إلى نوع آخر من الدوال، وهي الدوال الكسرية.

مواضيع ذات صلة

مشتق الدوال الثابتة : Differntiation Of Constant Functions

اشتقاق جمع وطرح الدوال : Differentiation of Sums and Differences

معادلة خط المستقيم المماس للمنحنى : Equations Of Tangent Lines

ضبط رموز المشتقات : Notations For Derivatives

تعريف مشتق الدالة عند نقطة : DEFINTION OF DERIVATIVE OF FUNCTION IN POINT

الاشتقاق والتفاضل على (IR) DIFFERENTIATION AND DERIVATIVES IN IR

معادلة خط المستقيم المماس للمنحني : TANGENT LINES

نظرية القيم الوسطى : THE INTERMEDIATE – VALUE THEOREN

القيم العظمى والصغرى : EXTREMA – MAXIMA AND MINIMA

دوال كثيرات الحدود والدوال الكسرية : POLYNOMIALS AND RATIONAL FUNCTIONS

الاستمرارية: continuity

اتصال الدوال والاستمرارية CONTINUITY OF FUNCTIONS