An 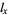 table is a tabulation of numbers which is used to calculate life expectancies.

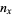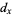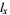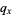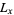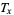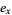0	1000	200	1.00	0.20	0.90	2.70	2.70
1	800	100	0.80	0.12	0.75	1.80	2.25
2	700	200	0.70	0.29	0.60	1.05	1.50
3	500	300	0.50	0.60	0.35	0.45	0.90
4	200	200	0.20	1.00	0.10	0.10	0.50
5	0	0	0.00	--	0.00	0.00	--
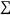		1000	2.70

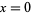: Age category (, 1, ..., 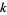). These values can be in any convenient units, but must be chosen so that no observed lifespan extends past category .

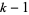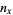: Census size, defined as the number of individuals in the study population who survive to the beginning of age category . Therefore, 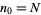 (the total population size) and .

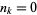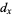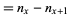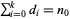: ; . Crude death rate, which measures the number of individuals who die within age category .

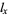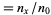: . Survivorship, which measures the proportion of individuals who survive to the beginning of age category .

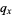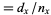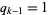: ; . Proportional death rate, or "risk," which measures the proportion of individuals surviving to the beginning of age category  who die within that category.

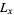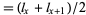: . Midpoint survivorship, which measures the proportion of individuals surviving to the midpoint of age category . Note that the simple averaging formula must be replaced by a more complicated expression if survivorship is nonlinear within age categories. The sum 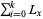 gives the total number of age categories lived by the entire study population.

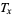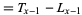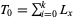: ; . Measures the total number of age categories left to be lived by all individuals who survive to the beginning of age category .

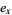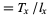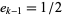: ; . Life expectancy, which is the mean number of age categories remaining until death for individuals surviving to the beginning of age category .

For all , 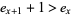. This means that the total expected lifespan increases monotonically. For instance, in the table above, the one-year-olds have an average age at death of 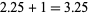, compared to 2.70 for newborns. In effect, the age of death of older individuals is a distribution conditioned on the fact that they have survived to their present age.

It is common to study survivorship as a semilog plot of 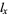 vs. , known as a survivorship curve. A so-called 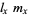 table can be used to calculate the mean generation time of a population. Two  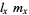tables are illustrated below.

Population 1

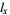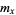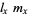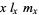0	1.00	0.00	0.00	0.00
1	0.70	0.50	0.35	0.35
2	0.50	1.50	0.75	1.50
3	0.20	0.00	0.00	0.00
4	0.00	0.00	0.00	0.00

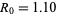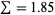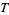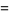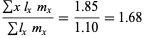			(1)
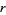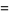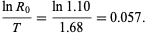			(2)

Population 2

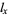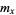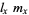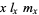0	1.00	0.00	0.00	0.00
1	0.70	0.00	0.00	0.00
2	0.50	2.00	1.00	2.00
3	0.20	0.50	0.10	0.30
4	0.00	0.00	0.00	0.00

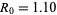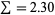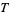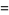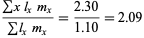			(3)
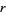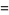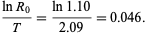			(4)

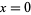: Age category (, 1, ..., 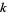). These values can be in any convenient units, but must be chosen so that no observed lifespan extends past category  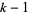(as in an  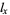table).

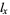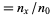: . Survivorship, which measures the proportion of individuals who survive to the beginning of age category  (as in an 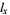 table).

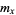: The average number of offspring produced by an individual in age category  while in that age category. 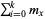 therefore represents the average lifetime number of offspring produced by an individual of maximum lifespan.

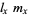: The average number of offspring produced by an individual within age category  weighted by the probability of surviving to the beginning of that age category. 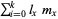 therefore represents the average lifetime number of offspring produced by a member of the study population. It is called the net reproductive rate per generation and is often denoted .

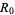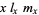: A column weighting the offspring counted in the previous column by their parents' age when they were born. Therefore, the ratio  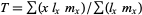is the mean generation time of the population.

The Malthusian parameter 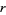 measures the reproductive rate per unit time and can be calculated as 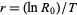. For an exponentially increasing population, the population size  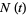at time  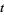is then given by

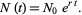(5)

In the above two tables, the populations have identical reproductive rates of 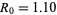. However, the shift toward later reproduction in population 2 increases the generation time, thus slowing the rate of population growth. Often, a slight delay of reproduction decreases population growth more strongly than does even a fairly large reduction in reproductive rate.

REFERENCES:

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 294-295, 1999.