

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Kermack-McKendrick Model
المؤلف:
Anderson, R. M. and May, R. M
المصدر:
"Population Biology of Infectious Diseases: Part I." Nature 280
الجزء والصفحة:
...
21-12-2021
1585
Kermack-McKendrick Model
The Kermack-McKendrick model is an SIR model for the number of people infected with a contagious illness in a closed population over time. It was proposed to explain the rapid rise and fall in the number of infected patients observed in epidemics such as the plague (London 1665-1666, Bombay 1906) and cholera (London 1865). It assumes that the population size is fixed (i.e., no births, deaths due to disease, or deaths by natural causes), incubation period of the infectious agent is instantaneous, and duration of infectivity is same as length of the disease. It also assumes a completely homogeneous population with no age, spatial, or social structure.
The model consists of a system of three coupled nonlinear ordinary differential equations,
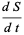 |
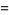 |
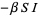 |
(1) |
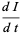 |
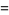 |
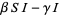 |
(2) |
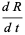 |
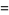 |
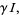 |
(3) |
where 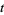 is time,
is time, 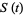 is the number of susceptible people,
is the number of susceptible people, 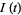 is the number of people infected,
is the number of people infected, 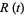 is the number of people who have recovered and developed immunity to the infection,
is the number of people who have recovered and developed immunity to the infection, 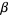 is the infection rate, and
is the infection rate, and 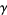 is the recovery rate.
is the recovery rate.
The key value governing the time evolution of these equations is the so-called epidemiological threshold,
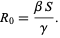 |
(4) |
Note that the choice of the notation 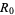 is a bit unfortunate, since it has nothing to do with
is a bit unfortunate, since it has nothing to do with 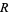 .
. 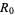 is defined as the number of secondary infections caused by a single primary infection; in other words, it determines the number of people infected by contact with a single infected person before his death or recovery.
is defined as the number of secondary infections caused by a single primary infection; in other words, it determines the number of people infected by contact with a single infected person before his death or recovery.
When 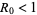 , each person who contracts the disease will infect fewer than one person before dying or recovering, so the outbreak will peter out (
, each person who contracts the disease will infect fewer than one person before dying or recovering, so the outbreak will peter out (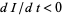 ). When
). When 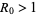 , each person who gets the disease will infect more than one person, so the epidemic will spread (
, each person who gets the disease will infect more than one person, so the epidemic will spread (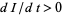 ).
). 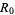 is probably the single most important quantity in epidemiology. Note that the result
is probably the single most important quantity in epidemiology. Note that the result 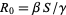 derived above, applies only to the basic Kermack-McKendrick model, with alternative SIR models having different formulas for
derived above, applies only to the basic Kermack-McKendrick model, with alternative SIR models having different formulas for 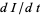 and hence for
and hence for 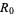 .
.
The Kermack-McKendrick model was brought back to prominence after decades of neglect by Anderson and May (1979). More complicated versions of the Kermack-McKendrick model that better reflect the actual biology of a given disease are often used.
REFERENCES:
Anderson, R. M. and May, R. M. "Population Biology of Infectious Diseases: Part I." Nature 280, 361-367, 1979.
Jones, D. S. and Sleeman, B. D. Ch. 14 in Differential Equations and Mathematical Biology. London: Allen & Unwin, 1983.
Kermack, W. O. and McKendrick, A. G. "A Contribution to the Mathematical Theory of Epidemics." Proc. Roy. Soc. Lond. A 115, 700-721, 1927.
Wolfram Research, Inc. "Kermack-McKendrick Disease Model." http://library.wolfram.com/webMathematica/Biology/Epidemic.jsp.















 قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر كتاب (سر الرضا) ضمن سلسلة (نمط الحياة)
قسم الشؤون الفكرية يصدر كتاب (سر الرضا) ضمن سلسلة (نمط الحياة)

















