


تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الموجات وعدم اليقين الكمي
المؤلف :
فرانك كلوس
المصدر :
العدم
الجزء والصفحة :
الفصل السابع (ص93- ص97)
2023-02-06
1804
ميكانيكا الكم كلها مبنية على خاصية أساسية واحدة للطبيعة: هي أنه يستحيل قياس كل من موضع الجسيم وزخمه بدقة تامة. فإذا عرفت الموضع تمام المعرفة، فأنت إذن لا تعرف شيئا البتة عن زخمه، والعكس صحيح. لكن إجمالا هناك حل وسط. فإذا كان معروفا أن موضع جسيم ما يقع داخل نطاق مسافة قدرها r من نقطة ما، فلا بد إذن أن يكون زخمه غير معروف على الأقل بالمقدار p حيث:

وħ هي ثابت الطبيعة الذي يعرف باسم «ثابت بلانك» (مقسوما فعليا على 2π).
تنطق ħ «إتش بار»، ومقدارها هو
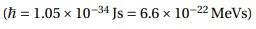
وهذا المقدار غاية في الصغر لدرجة يستحيل معها مقارنته بالأشياء المرئية، لكن فيما يخص الذرات ومكوناتها فهو الذي يحكم سلوكها.
ثمة عدم يقين مشابه بخصوص الزمن والطاقة (ذكرت سابقا أن ميكانيكا الكم مبنية على خاصية أساسية «واحدة» لأن عدم اليقين بشأن الموضع والزخم يقابله في الزمكان عدم اليقين بشأن الزمن والطاقة). يعني هذا أن مبدأ حفظ الطاقة يمكن «انتهاكه» على مدار مقاييس زمنية قصيرة للغاية. وضعت كلمة «انتهاك» بين علامتي اقتباس لأنه من المستحيل أن يلاحظه المرء؛ فهذا هو لب عدم القدرة على تحديد الطاقة «على وجه الدقة» في أي وقت بعينه. يمكن للجسيمات أن تشع طاقة (على شكل فوتونات على سبيل المثال) في انتهاك ظاهر لمبدأ حفظ الطاقة، ما دامت جسيمات أخرى تعيد امتصاص هذه الطاقة على مدار فترة زمنية قصيرة. وكلما أفرط في السحب من رصيد الطاقة قصر الزمن الذي لا بد أن تسترد الطاقة فيه؛ فكلما سحبت على المكشوف من حسابك البنكي زاد احتمال أن يلاحظ البنك ذلك بسرعة، وتعين عليك أن تسدد المال قبل أن يكتشف الأمر وبهذا يكون الكل راضيًا. يلعب هذا الانتهاك «الافتراضي» لمبدأ حفظ الطاقة دورا مهما في نقل القوى بين الجسيمات. في الصورة الكمية للمجال الكهرومغناطيسي، يكون هذا الانتقال على صورة فوتونات افتراضية، أو حزم كمية، أو «جسیمات» ضوئية، تطير عبر الزمكان وتنقل القوى إلى الأجسام البعيدة.
لاحظ كيف استخدمت كلمة «فوتونات» باعتبارها «جسیمات» ضوئية هنا. أليس الضوء موجة؟ ترجع الطبيعة المزدوجة للضوء بوصفه موجة أو جسيما إلى إسحاق نيوتن. تعمل أشعة الضوء كما لو كانت مكونة من تيارات من الجسيمات؛ فهي تنتقل في خطوط مستقيمة، وتترك ظلالًا حادة، وتنحرف عند التقائها بأوساط مختلفة كما يحدث عند التقائها بالهواء والزجاج، طبقا لقواعد البصريات الهندسية التقليدية. ومع ذلك يظهر الضوء أيضا خصائص شبيهة بخصائص الموجات؛ فحواف الظلال غير حادة، وحين يتشتت الضوء عبر ثقوب صغيرة يمكن أن تظهر حزما معتمة وأخرى مضيئة تعرف ب «هدب التداخل». إن الحقيقة القائلة إنه يمكن في ظل ظروف معينة لشعاعين متداخلين من الضوء أن يلغي أحدهما الآخر بحيث ينتج ظلام يمكن أن يسهل فهمها إذا تعاملنا مع الضوء بوصفه موجة؛ فعندما تتزامن قمتان تكون هناك قمة كبيرة، أو سطوع شديد، لكن عندما تلتقي قمة وقاع فإن أحدهما يلغي الآخر فيكون ظلام.
في عام 1900 أثبت ماكس بلانك أن الضوء ينبعث في «حزم» أو «كموم» ميكروسكوبية منفصلة من الطاقة تعرف بالفوتونات، وفي عام 1905 أثبت أينشتاين أن الضوء يظل على صورة الحزم هذه وهو ينتقل عبر الفضاء. وقد قدم بلانك في نظريته حول كموم الطاقة «ثابت بلانك» الذي يحمل اسمه، والذي يشار له بالرمز ħ (أما 2π/ħ فيشار إليه بالرمز ħ). وكانت هذه بداية نظرية الكم وكان سبب نجاحها الفوري هو تفسيرها للكيفية التي توجد بها الذرات.
على ما يبدو يدور الإلكترون داخل ذرة الهيدروجين حول البروتون المركزي بسرعة 137/1 من سرعة الضوء. ويعني دورانه في مدار طوله 10-9 أمتار بسرعة حوالي ألف كيلومتر في الثانية أنه يقطع نحو مليون المليار لفة في الثانية. طبقا لنظرية ماكسويل، ينبغي أن يبث مثل هذا الإلكترون إشعاعا كهرومغناطيسيا على الفور، بحيث إنه في اللحظة التي تتكون فيها هذه الذرة يسقط الإلكترون للتو في حركة حلزونية نحو النواة ليتلاشيا في وهج من الضوء. كيف إذن توجد الذرات؟ كان اكتشاف أن الطاقة المشعة. هي طاقة كمية هو الذي قاد نيلز بور إلى أن يقترح أن طاقات الإلكترونات داخل الذرات كمية هي أيضا؛ فلا يمكنها أن تملك سوى طاقات محددة. ولما كانت الإلكترونات محصورة في حالات الطاقة المحددة هذه، فإنها لا تبث الطاقة باستمرار ولا تسقط حلزونيا نحو النواة. وإنما يمكنها فقط أن تقفز من إحدى حالات الطاقة إلى أخرى، وتشع الطاقة أو تمتصها كي تحفظ إجمالي مقدار الطاقة ثابتا (عبر فترات زمنية طويلة تحفظ الطاقة). وبمجرد أن تصير الإلكترونات في حالة الطاقة الدنيا، لن يكون لديها مكان أدنى لتذهب إليه، ومن ثم تظل هناك مكونة ذرة مستقرة. قد تظن أن هذا الحل غير واقعي؛ إذ إنه يقضي بأن الذرة تصير مستقرة لأنها مستقرة. غير أننا إذا تقبلنا مفهوم الموجة فمن الممكن أن نتخيل السبب.
اقترح بور أن ثابت بلانك ħ يحكم الطاقات المسموح بها للإلكترون الذي يدور داخل الذرة. في الصورة الحديثة، ليس الضوء وحده فحسب وإنما الإلكترون أيضا يتمتع بخصائص أشبه بالموجات، ويرتبط طوله الموجي وزخمه بنفس الكمية ħ. الآن طبق هذه الفكرة على ذرة الهيدروجين، أبسط ذرة، التي تملك إلكترونا واحدا فحسب. تلغي موجات الإلكترون بعضها بعضا وتتبدد في أي مسارات لا «تتوافق» فيها. هذا موضح في الشكل 7-1. في الجزء (أ) نرى إلكترونا يتحرك بطول المسار، وهو يمثل على شكل موجة. الآن تخيل الطول الموجي الكامل وقد أخذ شكل دائرة. عندما تناسب الموجة الدائرة بالضبط، يكون هذا أول مدار ممكن، وإذا لم تتناسب الموجات على هذا النحو فإنها تتلاشى. يكون الطولان الموجيان اللذان يكملان الدائرة كما في الشكل 7-1 (ب) مدار بور الثاني الذي يتمتع بطاقة أعلى من المدار الأول، وتتوافق المدارات ذات الطاقة الأعلى مع عدد أكبر من الأطوال الموجية الموجودة في محيط الدائرة (شكل ۷-۱ (ج)). واللافت للنظر أن هذه الصورة المبسطة تتطابق مع ما نعرفه عن الذرات.
لا تنبعث أي طاقة عندما يظل الإلكترون في مداره، لكن الطاقة تنبعث إذا قفز الإلكترون من حالة أعلى من الطاقة إلى حالة أدنى. وبافتراض أن هذه الطاقة المنبعثة حولت إلى ضوء، حسب بور الأطوال الموجية المرتبطة ووجد أنها تتوافق بالتمام مع طيف الهيدروجين الغامض. وهكذا فإن نظرية الكم لبلانك، التي انطبقت بنجاح على الإشعاع عندما افترض أينشتاين وجود الفوتون، انطبقت بنجاح مماثل على المادة على يد بور.
من الملامح الجوهرية لهذا أن نظرية الكم باتت تقضي بأن ثنائية الموجة-الجسيم خاصية لكل صور المادة؛ فالإلكترون الذي نفكر فيه على أنه جسيم، هو فعليا حزمة كمية من «مجال إلكتروني» يملك خصائص تشبه الخصائص الموجية. وبقدر ما يبدو هذا غريبا، فهذه هي الحقيقة: إذ تعتمد المجاهر الإلكترونية على هذه الخاصية شبه الموجية للإلكترونات.
ما هذه الموجات؟ وكيف ترتبط بمبدأ عدم اليقين الذي تناولناه سابقا؟ أزعجت أسئلة كهذه العلماء أيما إزعاج منذ بزوغ نظرية الكم. استفاض كل من أينشتاين وبور، ضمن كثيرين، في مناقشة معنى نظرية الكم.

شكل 7-1: موجات الإلكترونات في نموذج بور الذري.
على المستوى المبدئي، على المرء أن يقبل فحسب بمبدأ عدم اليقين وتبعاته. غير أن الأمر يكون أكثر راحة دائما عندما نستطيع أن نبني نموذجا فكريا يجسد خصائص النظرية، لأننا عندئذ نستطيع أن ننمي حدسنا بشأن سلوكها وتبعاتها. يمكن تشبيه عدم اليقين الخاص بالموضع والزخم بشيء نألفه؛ ارسم الكثير من النقاط بحيث تكون شكل موجة لها طول موجي ثابت؛ عندئذ إذا حددنا الموضع باعتباره مكان نقطة معينة في الموجة والزخم باعتباره الطول الموجي؛ يصير لدينا تشبيه جيد لمبدأ. عدم اليقين على أرض الواقع. طبقا لميكانيكا الكم، كلما زاد الزخم قصر الطول الموجي. افترض أنني أعرف الموضع بالضبط سيكون إذن كل ما لدي هو نقطة واحدة، وسيكون من المستحيل معرفة مقدار الطول الموجي؛ فمن الممكن أن يكون بأي قيمة تريدها. وإذا كان لدي عدد قليل من النقاط يشكل بداية موجة، عندئذ سأبدأ في اكتشاف هل الطول الموجي طويل أم قصير، وفقط بعدما يكون لدي طول موجي كامل، سأتمكن من أن أحدد بكل يقين مقدار قیمته. غير أن ثمن هذا اليقين حيال معرفة الطول الموجي سيكون التخلي عن معرفة الموضع المحدد على امتداد الطول الموجي بأي درجة من الدقة. يتحقق هذا حسابيًا من خلال تحليل فورييه، وهو تمثيل أي انحناء، أو حتى ارتفاع حاد، على صورة تراكب لموجات ذات أطوال موجية مختلفة. يساوي الارتفاع المنفرد في موضع محدد مجموع عدد لانهائي من الموجات ذات الأطوال الموجية المختلفة.
نرى هنا نوعا من التناقض في القول إننا نحاول تحديد موضع إحدى الموجات؛ إذ إن الموجة لا تصبح موجة معروفة إلا عندما نقيس طولها الموجي الكامل. إذا أقنعك هذا المثال بالقبول بأن ثمة مواقف أخرى يستحيل فيها تحديد الموضع وخاصية أخرى بدقة على نحو ذي مغزى، فأنت في طريقك لفهم طبيعة عالم الكم. إن تمتع الموجات بمثل هذه الخصائص يجعلها مفيدة للغاية باعتبارها نماذج فكرية تعبر عما يحدث في الواقع. غير أنها في رأيي لا تتجاوز هذا؛ مجرد نماذج فكرية.