لقد بينت الدراسات الإحصائية أن المنحنيات البيانية لتوزيعات كثير من الظواهر الطبيعية المختلفة ، على مجموعة عشوائية كبيرة من النتائج تأخذ شكلاً قريباً من عمل المنحني الطبيعي ، ذي القمة الواحدة والمتماثل حول محور يمر بقمته . والصورة العامة لمعادلة المنحني الطبيعي هي :

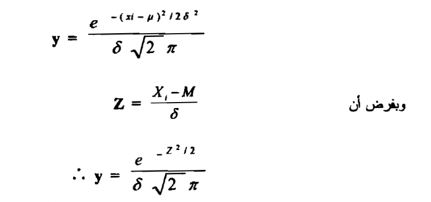
 وبفرض أن حيث X هي قيمة المشاهدة الواحدة ،M هي المتوسط الحسابي الحقيقي ( X - M ) هو الانحراف عن المتوسط الحسابي الحقيقي y و هي تكرار قيم

  ( x - M ) و 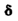هي الانحراف المعياري ، ويطلق على Z اسم القيمة المعيارية .

ومن الجدير بالذكر أن المساحة تحت هذا المنحني تساوي الوحدة ( أي واحد صحيح ) وهناك جداول معدلتبين المساحة تحت هذا المنحني والمحصورة بين   الى Z حيث Z مقدار موجب ، أي المساحة تحت المنحني الواقعة الى يسار القيمة المعيارية  X

مثال ( 6 ) :-

تم تحليل 3000 عينة ، حيث أخذت نتائج التحليل شكلاً قريباً من التوزيع الطبيعي وكان الوسط الحسابي 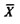   لهذه النتائج يساوي 170 نانوجراماً / لتر ، والإنحراف المعياري لها يساوي 5 . احسب :

 -1 نسبة العينات التي تزيد محتواها علي 185 نانوجراماً / لتراً .

 -2 عدد العينات التي يزيد محتواها عن 185 نانوجراماً / لتراً .

الحل :-

(1)  نحول القيم الخام الي قيم معيارية باستخدام القانون

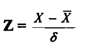
فنجد أن القيمة المعيارية للتركيز 185 نانوجراماً / لتراً -

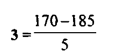
وحيث أن نسبة المساحة تحت Z = 3 هي 0.9987

إذا نسبة المساحة فوق Z = 3هي 0.0013 -0.9987 -1 = % 0.13

وهذا يعني أن نسبة العينات التي يزيد علي 185 نانوجراماً / لتراً هي 0.13 %

( 2 ) بما أن نسبة العينات التي يزيد التركيز فيها على 185 نانوجراماً / لتراً .

0.13 %  فإن عدد العينات يساوي .

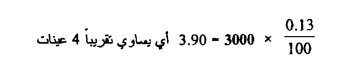
 اختبار Q-Test - : Q 

عند إجراء تحليل ما ، قد نجد أن نتيجة من النتائج تبتعد عن بقية النتائج ، مـــن المحتمل أن تكون هذة النتيجة خاطئة ، ولكن كيف يمكن إهمال هذه النتيجة أو اعتمادها ؟ ولاجراء اعتماد نتيجة من النتائج أو إهمالها نلجأ الي اختبار عرف باختبارQ (Q-Test) حيث يتم في هذا الإختبار ترتيب النتائج ترتيباً تصاعدياً وتعطي رموزاً للدلالة عليها مثل  

 ( X . ..... X₁ X₂, X₃) ولاختبار أقل نتيجة نطبق العلاقة:

وعند اختبار أعلى نتيجة تطبق العلاقة :

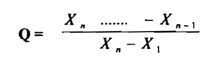
وتقارن القيم المتحصل عليها مع قيم مثالية معدة في جداول خاصة فإذا كانت قيمة Q >المثالية الحسابية فإن النتيجة تثبت ، أما إذا كانت النتيجة أن قيمة Q المثالية<   Q الحسابية فتلغي النتيجة ويتم إهمالها

جدول : قيم Q المثالية عند مستوي الثقة 90%

ومن الجدير بالذكر أن اختبار Q يطبق في البداية على أكبر قيمة وأصغرها ، فإذا حذفت إحداهما نطبق الإختبار علي القيمة التي تليها ، وهكذا .

مثال (7 ) :

 عند معايرة حامض الهيدروكلوريك مع هيدروكسيد الصوديوم والمعروف العيارية سجلت النتائج التالية لمعيارية الحامض

0.1014, 01018, 0.1015, 0.1019, 0.1021, 0.1025, 0.1059

اوجد أي القيم يمكن الإحتفاظ بها ، وأي القيم يمكن اهمالها

الحل :

وبمقارنة هذه القيمة مع القيمة المثالية من جدول قيم Q المثالية عند مستوي الثقة 90 % عندما يكون عدد القراءات يساوي 7 نجد أن Q المثالية تساوي 0.15

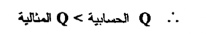
إذا هذه القيمة أكبر من القيمة المثالية، وعليه تحذف هذه القراءة ، ونختبر القيمة التــي تليها ( القيمة 0.1025 )

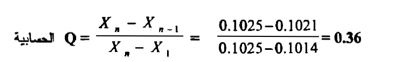
وبقارنة هذة القيمة مع القيمة المثالية من الجول ( 4.13) عندما يكون عدد القراءات يساوي 6 ؛ حيث حذفت القيمة العليا نجد أن :

مواضيع ذات صلة

نظام استخلاص الجزئيات البسيطة

اختيار الطور الجديد وعدد مرات الاستخلاص

ميكانيكية الاستخلاص

طبيعة الصنف المستخلص

الاستخلاص بالمذيب

امتصاص الشعاع الكهرومغناطيسي وطيف الامتصاص

الطرق الكيميائية الطيفية في التحليل.

طبيعة الكيمياء التحليلية

التحليل بالحقن الجرياني المتقطع Batch flow injection analysis

الحقن الجرياني متعدد التخفيف Multi-commutation in FIA

التحليل بالحقن المتعاقب Sequential Injection Analysis

التحليل بالجريان المتقطع Segment Flow Analysis