أن دراسة العلاقة بين ظاهرتين أو متغيرين ، ومعرفة مقدار هذه العلاقة أمر هام جداً في الحياة العملية ، وعلى الأخص للباحثين ، والمخططين ، وتسمي العلاقة متغيرين بالإرتباط ، وتقاس درجة العلاقة بين متغيرين يأخذ من القيم المحصورة بيـــن ( - 1 ، + 1 ) فإذا رمزنا لمعامل الارتباط بالرمز R فإن

[ ( - 1 ، + 1 ) Rε ]    

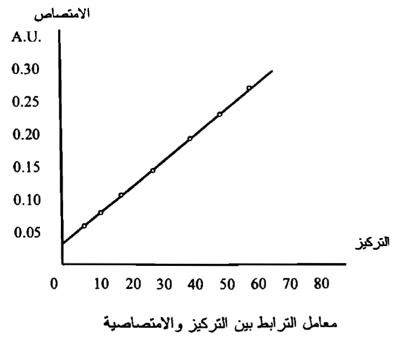
ومن السهل تكوين فكرة عن العلاقة بين متغيرين بيانياً ؛ حيث يمكــن رســــم الإحداثيين x و y الذين يمثلان المتغيرين ، ويسمي الشكل الناتج شكل الإنتشار ، فإذا أمكن تمثيل مجموعة النقط الممثلة للمتغيرين في هذا الشكل بخط مستقيم – حيث تكون هذة النقط قريبة من الخط المستقيم - كانت العلاقة ( بين المتغيرين ) قوية ، وإذا كانت النقط مبعثرة ، ولا يمكن تمثيلها بخط مستقيم كانت العلاقة بين المتغيرين ضعيفة .

ويكون معامل اللإرتباط موجباً إذا كان المتغير في الظاهرتين يسير في نفس الإتجاه ، وفي هذه الحالة نجد أنه إذا زادت قيمة أحد المتغيرين تزداد قيمة المتغير الثاني ، وإذا قلت قيمة أحد المتغيرين تقل قيمة المتغير الثاني ، ويقال لمثل هذا الإرتباط الطردي ، ويكون الارتباط سالباً إذا كان التغيير في إحدي الظاهرتين يسير في اتجاه معاكس لإتجاه التغير في الظاهرة الأخري ، أي إذا زادت قيمة أحد المتغيرين قلت قيمة المتغير الثاني ، ويدعي هذا الارتباط العكسي . عند حساب قيمة معامل الارتباط ، فإذا كانت قيمته +0.9 فيعبر هذا عن علاقة قوية بين متغيرين ، ومعامل الارتباط + 0.5 يعبر عن علاقة متوسطة ، أما معامل الارتباط + 0.2 فيعبر عن علاقة ضعيفة . ويمكن حساب قيمة معامل الارتباط بين المتغيرينY X, بإستخدام العلاقة الرياضية التالية :

وقيمة معامل الارتباط هذه تشير الي ترابط وعلاقة قوية جداً بين التركيز والامتصاصية ، وعند رسم هذه العلاقة بيانياً نلاحظ أن معظم النقاط تقع مستقيم ، كما في الشكل التالي :

مواضيع ذات صلة

نظام استخلاص الجزئيات البسيطة

اختيار الطور الجديد وعدد مرات الاستخلاص

ميكانيكية الاستخلاص

طبيعة الصنف المستخلص

الاستخلاص بالمذيب

امتصاص الشعاع الكهرومغناطيسي وطيف الامتصاص

الطرق الكيميائية الطيفية في التحليل.

طبيعة الكيمياء التحليلية

التحليل بالحقن الجرياني المتقطع Batch flow injection analysis

الحقن الجرياني متعدد التخفيف Multi-commutation in FIA

التحليل بالحقن المتعاقب Sequential Injection Analysis

التحليل بالجريان المتقطع Segment Flow Analysis