
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
المجموعات النقطية (الطوائف) Point Groups
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص21–27
2023-09-17
2032
هناك اثنتان وثلاثون مجموعة بلورية تسمى المجموعات النقطية أو الطوائف البلورية، وتعود التسمية إلى أن جميع عمليات التماثل فيها تعيد التركيب البلوري إلى ما كان عليه قبل إجراء تلك العمليات بينما تظل نقطة واحدة ثابتة بدون تغيير.
وقد تحتوي الطوائف البلورية النقطية على الأنواع التالية من عمليات التماثل:
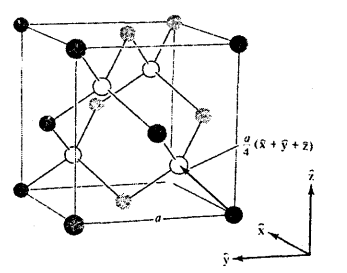
شكل (7-1)
خلية مكعبية نموذجية لشبيكة الألماس والمواقع غير المظللة تنتمى لإحدى الشبيكتين المتداخلتين
1- الدوران خلال مضاعفات صحيحة للزاوية π/n2 حول محور دوران ذي n طية. وقد وجد أن شبيكات براقيه يمكنها أن تحتمل وجود محاور ذات طيتين أو ثلاث أو أربع أو ست طيات فقط، وحيث إن المجموعات النقطية تقع في نطاق شبيكات براقيه فهي الأخرى لا تحتوي إلا على هذه المحاور.
2- الدوران – الانعكاسي، وفيه يكون عنصر التماثل يشمل دورانا بزاوية مقدارها π/n2 ومصحوبا بانعكاس في مستوى (كالمرآة) متعامد مع المحور. وبهذا يصبح لدينا محور دوران انعكاسي ذو n- طية.
3- الدوران الانقلابي، وفيه يتم دوران بزاوية مقدارها π/n2 يعقبه انقلاب في نقطة تقع على محور الدوران الذي عندئذ محور دوران انقلابي يسمى ذا n- طية.
4- الانعكاس، وفيه تتحول كل نقطة إلى صورتها في مرآة يمثلها مستوى يعرف بالمستوى المراوي.
5- الانقلاب، وتحدث هذه العملية خلال نقطة ثابتة هي مركز الانقلاب بحيث تتحول أية نقطة يحددها المتجه 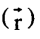 إلى نقطة يحددها متجه آخر هو
إلى نقطة يحددها متجه آخر هو
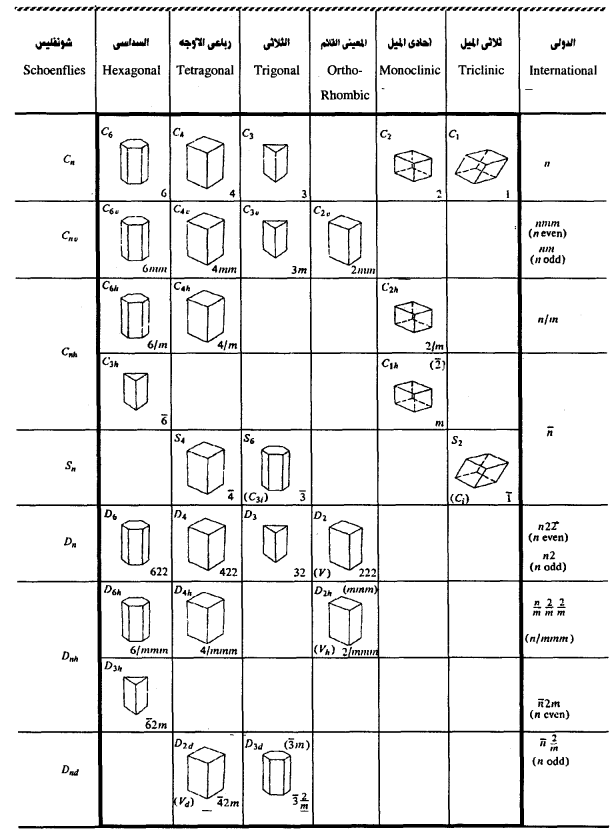
وتوصف المجموعات النقطية من خلال تسميات مختلفة من أشهرها تلك التي ابتكرها «شونفليس» إلى جانب التصنيف الدولي. وكلتا التسميتين موضحة في الجدولين
1-3، 1-4.
جدول (1-3)
المجموعات البلورية النقطية غير المكعبية
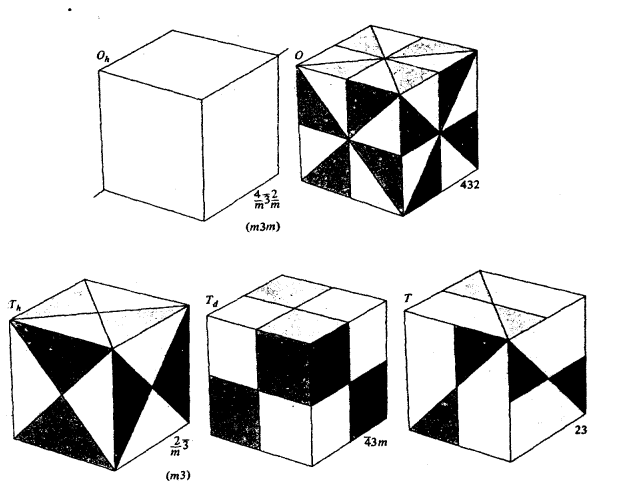
جدول (1-4)
المجموعات النقطية المكعبية.
تصنيف «شونفليس»
Cn: لا تحتوي هذه المجموعات أو الطوائف إلا على محور دوران ذي n طية؛ حيث n= 1, 2, 3, 4, 6
الدوران، محور
Cnv: تحتوي هذه الطوائف على مستوى مرآوي يمر بداخله محور الدوران، بالإضافة إلى عدد من المستويات التي يحددها المحور الرئيسي.
Sn: تحتوي هذه الطوائف على محور دوران انعكاسي ذي n- طية.
Dn: تحتوي هذه الطوائف على محور ذي طيتين، يتعامد مع محور ذي n- طية، بالإضافة إلى محاور ذات طيتين يحدد عددها المحور الرئيسي.
nhD: تعتبر هذه الطوائف من النوع الأكثر تماثلا حيث تحتوي على جميع عناصر تماثل المجموعة Dn مضافا إليها مستوى مرآوي متعامد مع المحور الرئيسي.
Dnd: تحتوي هذه الطوائف على عناصر تماثل المجموعة Dn مضافا إليها مستويات مراوية تضم المحور الرئيسي الذي ينصف الزاوية الواقعة بين المحورين الثنائيين (كل محور منها ذو طيتين).
التصنيف الدولي للطوائف غير المكعبية
هناك ثلاث طوائف ينطبق تصنيفها الدولي مع تصنيف «شونفليس» وهي:
n : وهي تقابل الطائفة Cn.
: nmm وهي تقابل Cnv
ويشير حرفا m إلى نوعين محددين من المستويات المراوية التي تحتوي على محور ذي nطية وتتمثل هذه الطوائف في الأجسام التي توصف بالرموز 6mm، 4mm، 2mm ومعنى هذا أن المحور الرئيسي يؤدي إلى ظهور مستويات أخرى عددها هو عدد الطيات للمحور. والمجموعة (الطائفة) m3 تناظر المجموعة C3v؛ أي أن المحور الرئيسي (3) ينتج ثلاثة مستويات.
2 2 n: وهي تقابل Dn حيث تتعامد المحاور ذات الطيتين مع المحور الرئيسي.
أما العلاقة بين بقية الطوائف الدولية وطوائف «شونفليس» فهي كما يلى:
n/m: وهي تناظر Cnh فيما عدا أن التصنيف الدولي يعتبر C3h على أنها تحتوي على محور ذي ست طيات (سداسي) ويكون محور دوران انقلابي، أي ̅6. كما أن C1h هو ببساطة m بدلا من m/1.
n̅: تحتوي هذه الطائفة على محور دوران انقلابي ذي n- طية وتضم هذه الطائفة S4 التي تؤول إلى ̅4 بشكل جيد أما S6، فتصبح ̅3 وS4 تصبح̅1 وذلك في ضوء الفرق بين محاور الدوران الانقلابية ومحاور الدوران الانعكاسية.
n/m 2/m 2/m: وتكتب مختصرة هكذا n/mmm وهي تناظر Dnh فيما عدا أن النظام الدولي يفضل اعتبار D3h على أنها تحتوي على محور دوران انقلابي ذي ست طیات (سداسي) فيصبح رمز الطائفة m2 ̅6. كما هو يلاحظ أن /mmm2 قد تكتب أحيانا mmm.
أي أن Dnh يمكن اعتبارها محتوية على محور ذي n- طية مع وجود مستوى مرآوي متعامد معه بالإضافة إلى مجموعتين متعامدتين معه من المحاور ذات الطيتين، بحيث يصبح لكل مجموعة المستوى المتعامد معها.
̅n 2 m: وهي تشبه Dnd فما عدا أن D3h تكون متضمنة في المجموعة m2 ̅6. ويشير هذا الرمز إلى وجود محور دوران انقلابي ذي n طية مع محور ذي طيتين متعامد معه، بالإضافة إلى مستوى مرآوي رأسي. ومرة أخرى تكون الحالة 3=n استثنائية ويصبح رمزها 2/m ̅3 (أو اختصارا m̅3) لكي يعبر عن أن المستوى الرأسي متعامد مع المحور ذي الطيتين.
تصنيف الطوائف النقطية البلورية المكعبية
يوضح الجدول 1-4 كلا من تصنيف «شونفليس» والتصنيف الدولي للطوائف المكعبية الخمس:
Oh: وهي تمثل الطائفة المكتملة للمكعب (أو ثمانية الأوجه، ومن هنا جاء الحرف O من كلمة (Octahedron بما فيها من العمليات غير السوية (أي التي تتحول فيها الأشكال يمينية اليد إلى أشكال يسارية اليد)، وفيما عدا ذلك فباقي العمليات سوية، وتعتبر العمليات التي بها عدد فردي من مرات الانقلاب أو الانعكاس غير سوية أيضا. وقد يوجد بهذه الطائفة أيضا مستوى انعكاس أفقي (h).
O: يرمز هذا الحرف إلى المجموعة المكعبية التي لا تتضمن أية عمليات تماثل غير سوية.
Td: هي مجموعة التماثل المكتملة لرباعي الأوجه المنتظم Tetrahedron شاملا كل العمليات غير السوية.
T: هذه هي مجموعة رباعي الأوجه المنتظم مع استبعاد كل العمليات غير السوية.
Th: وهي المجموعة الناتجة عن إضافة انقلاب إلى المجموعة T، يلاحظ عادة وجود الرقم 3 في المجموعات المكعبية في حالة التصنيف الدولي؛ والسبب هو وجود محور ثلاثي الطية في جميع المجموعات المكعبية.
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















