
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
حساب التركيب بمساعدة الجهود بين الذرات Calculation Structure with the help of atom- atom potentials
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص287–292
2023-10-02
1114
حيث إنه يمكن إهمال الطاقة الكهروستاتيكية وتأثيرها على طاقة الربط للشبكة البلورية فلذلك فإن حساب هذه الطاقة يمكن أن يقتصر على حساب الطاقة الناتجة عن تفاعلات فان درفال Van der Waals Interactions.
وباستخدام هذه الطريقة التقريبية تكون طاقة الربط الناتجة عن تفاعلات فان درفال هي مجموع طاقات المتجهات التي تربط الذرات المكونة لجزيء واحد بكل الذرات للجزيئات المجاورة أي أن:
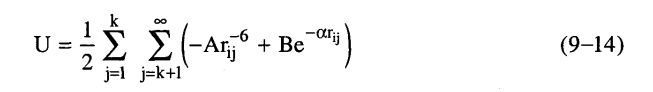
وبصفة عامة فإن القيم 6–rij Ʃ وαrij–e Ʃ يمكن حسابها باستخدام الحاسب الآلي وحيث إن طافة فان درفال تتناقص بازدياد المسافة فإنه يمكن إجراء الحسابات فقط للمسافات التي لا تزيد عن Å15 أو Å20، وقد أثبتت بعض الحسابات أنه في بعض البلورات العضوية يكون الخطأ في هذه الحالة لا يتعدى 0.1%، ومن المهم الإشارة إلى أنه في بعض الأغراض العملية يمكن أن يكون نصف القطر للتجميع أقل من ذلك، وتجب الإشارة إلى أنه نتيجة لبعض العمليات الفيزيائية التي تتضمن تشوها أو تمددا حراريا أو انضغاطا وغيرها يحدث تغيير في شكل وحجم الوحدة البنائية وكذلك ترتيب الجزيئات بالنسبة لبعضها البعض وتبعا لذلك يحدث تغير الطاقة الشبيكة البلورية ولكى نأخذ في الاعتبار هذه التغيرات سنقوم بتعريف طاقة الربط للشبيكة البلورية على أنها دالة متعددة الأبعاد للمتغيرات الآتية:
المسافات البينية للشبيكة البلورية γ، β، α،c ، b، a ثم زوايا أوليريان Eulerian angles ψ ،φ، θ وهي التي تحدد وضع الجزيء بالنسبة لمحاور البلورة ثم إحداثيات مركز ثقل الجزيء Z، X ، Y.
U = u (a, b, c, α, ẞ, γ, θ, φ, ψ, X, Y, Z)
وفي معظم الأحيان يمكن الافتراض أن الاختلافات في التغيرات السابقة لا تؤثر على ترتيب الذرات داخل الجزيء.
وبمعرفة شكل السطح متعدد الأبعاد يمكننا حساب بعض الخواص الطبيعية للبلورات نتيجة طاقة الربط للشبيكة البلورية عند نقطة النهاية الصغرى والتي يمكن تعيينها بدرجة من الدقة في حدود طاقة التذبذب عند نقطة الصفر zero point، فطاقة الربط عند النهاية الصغرى تساوي حرارة التبخير للبلورة عند نقطة الصفر المطلق (طاقة نقطة الصفر لمعظم البلورات الجزيئية لا تتعدى 1-2%) والتفاضل الثاني لطاقة الشبيكة البلورية بالنسبة للتشوه عند نقطة النهاية الصغرى للطاقة يعطينا معامل المرونة عند درجة الصفر (0 kº).
البلورات المكونة من ذرات من الكربون والأيدروجين تعتبر هدفا (object) مناسبا لاختبار دقة طريقة الجهود بين الذرات عندما تطبق على البلورات الجزيئية فكما ذكرنا من قبل يمكن إهمال مساهمة القوى الكهروستاتيكية وكذلك ذبذبة نقطة الصفر zero point oscillation في حرارة التبخير أو التسامي sublimation وكذلك في التركيب المتزن في مثل هذه البلورات وبذلك يكون سطح الربط الناتج من طاقة تفاعل فان درفال بمفرده هو الذي يفسر الخواص الطبيعية للبلورات بدرجة كبيرة من الدقة والحساب طاقة التفاعل للجزيئات الهيدروكربونية نحتاج لثلاثة منحنيات الطاقة التفاعل بين الذرات هي CC, CH, HH وفي المراحل الأولى لاختبار هذه الطريقة كتبت برامج على الحاسب الآلي لحساب طاقة الربط للشبيكة البلورية لبعض المركبات بمقارنة النتائج مع القيم العملية وفيما يلي بعض القيم:
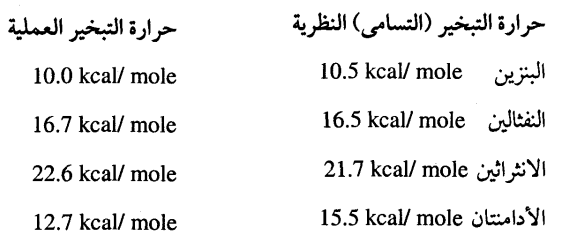
انظر شكل (16-9)، (17-9).

شكل (16-9)
شكل (17-9)
تعيين الوضع المتزن للجزيئات في الشبيكة البلورية بقيم معينة لأبعاد الوحدة البنائية
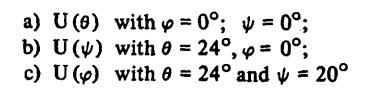
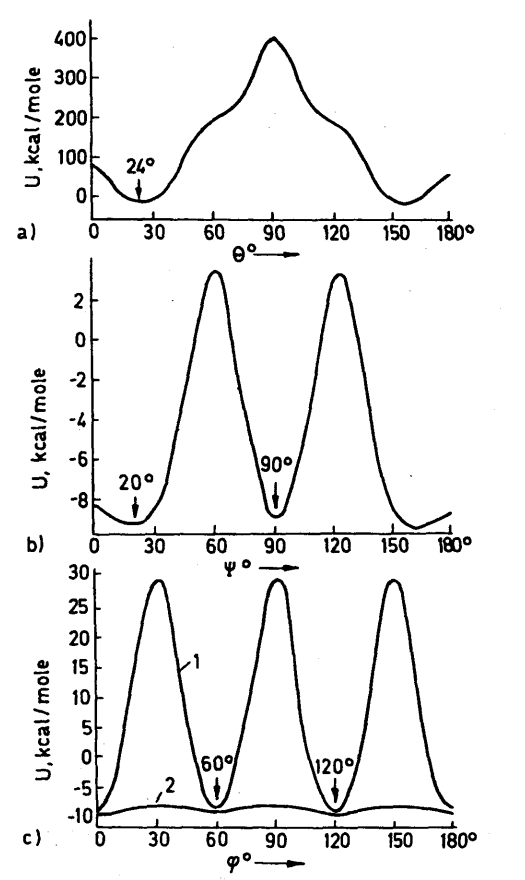
وإحداثيات النهاية الصغرى لسطح الطاقة الكلية مع كل المتغيرات يجب أن يكون في هذه الحالة أيضا تكون الجهود بين الذرية ممثلة لتركيب الشبيكة البلورية بدرجة كبيرة من الدقة ويوضح شكلا (18-9، 19-9) تغير الطاقة U مع c, b, a, ψ,φ ,θ وشكل (20-9) يوضح تغير قيمة U مع نصف قطر التجميع ولدراسة التركيب البلوري عند درجة الصفر المطلق يكون المطلوب قيمة النهاية الصغرى لسطح الطاقة عند القيم المتغيرة الست ألا وهي:
U = u (a, b, c, θ, φ, ψ)
وحسب المعنى الفيزيائي لهذه المتغيرات يمكن أن تنقسم إلى مجموعتين الأولى هي مجموعة زوايا تحدد ميل الجزيء على محاور الوحدة البنائية θ, φ, ψ Eulerian angles والثانية هي أطوال الوحدة البنائية a, b, c وكل من المجموعتين يمكن أن نبحث له عن النهاية الصغرى للطاقة بصورة منفردة (شكل 18-9، 19-9).

شكل (18-9)
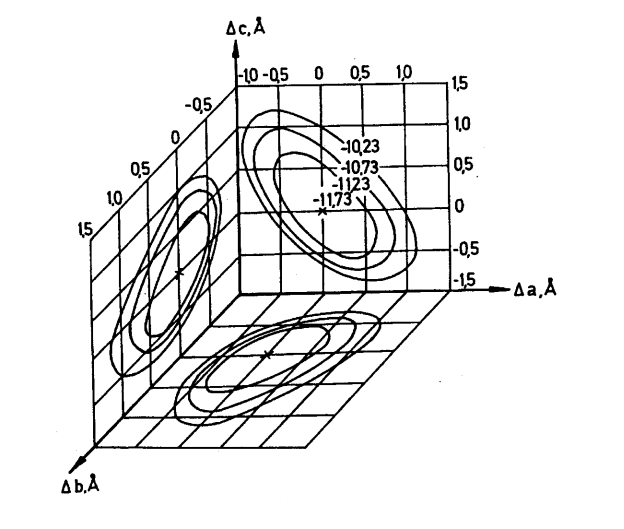
شكل (19-9)

شكل (20-9)
تغير طاقة الشبيكة البلورية لبلورات البنزين مع نصف قطر التجميع
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















