
تدقيق ريتفيلد: Rietveld Refinement
 المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
 المصدر:
علم البلورات والاشعة السينية
المصدر:
علم البلورات والاشعة السينية
 الجزء والصفحة:
ص326–330
الجزء والصفحة:
ص326–330
 2023-10-04
2023-10-04
 1378
1378
طريقة ريتفيلد في جوهرها ما هي إلا تدقيق بيانات حيود الأشعة السينية بطريقة المربعات الصغرى بحيث تصبح الفروق بين قيم شدة الأشعة المقاسة عمليا yi obs تلك المحسوبة باستخدام شكل للجسم المحدث للتشتيتyi calc أقل ما يمكن، وفي هذه الطريقة تعطى قيم لثقل هذه الفروق الفردية متناسبة مع مقلوب هذه الفروق يفترض في هذه الطريقة أن المادة عديدة التبلور متكونة من عدد كبير من البلورات المثالية وأن العينة لا تعاني من وجود اتجاه مفضل preferred orientation.
وتبعا لريتفيلد يعرف معامل المقياس كالآتي:

حيث ω1 هو الثقل المناسب ويعطى بالمعادلة:

ipσ هو الانحراف القياسي standard deviation الخاص بشدة الأشعة عند القمة (وهو في المعتاد يعتمد على حسابات إحصائية) ibσ هو ذلك الخاص بشدة المساهمات الأشعة الخلفية ((back ground، yic هو مجموع المساهمات من انعكاسات براج المجاورة بالإضافة للشدة الخلفية.

حيث s هو معامل القياس scale factor.
Lk هو معامل لورنتز والاستقطاب للانعكاس Fk ، k هو معامل التركيب، mk هو معامل التضاعف (multiplicity factor).

حيث 2θk هو الموقع المحسوب لقمة براج بعد إجراء التصويب الخاص بالنقطة الصفرية لكشاف الأشعة عليه، (Δθik) Gهي دالة الشكل الجانبي للانعكاس (reflection profile function).
المتغيرات التي يجب ضبطها بعملية التدقيق تشمل أبعاد الوحدة البنائية ومواقع الذرات والمتغيرات الحرارية والمتغيرات التي تعرف الدالة yib ، G.
وتعيين نموذج دقيق لدالة الشكل الجانبي (Δθik) Gهو أحد الأشياء الأساسية في حالات دراسة شكل الحيود سواء كان ذلك للقمم المفردة أو للشكل كله كما في حالة ريتفيلد، وقد أصبح ذلك حقيقة واضحة في الوقت الحاضر حيث أصبح من الممكن الحصول على التفاصيل في شكل الحيود باستخدام الأجهزة الحديثة، فشكل الحيود يعتمد على متغيرات عديدة مثل مصدر الأشعة وشكل العينة ونوع المكشاف. وتبعا لذلك فإنه توجد اختيارات كثيرة لشكل دالة الحيود هي:
1- في حالة إذا كان شكل الحيود يتبع توزيع جاوس (Gaussian) ...
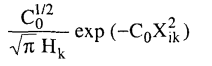
2- في حالة إذا كان شكل الحيود Lorentzian ...
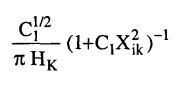
3- في حالة إذا كان شكل الحيود modif. 1 Lorentzian
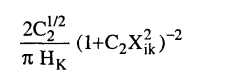
4- في حالة إذا كان شكل الحيود modif. 2 Lorentzian ...
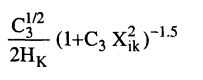
5- في حالة إذا كان شكل الحيود pseudo - Voigt ...
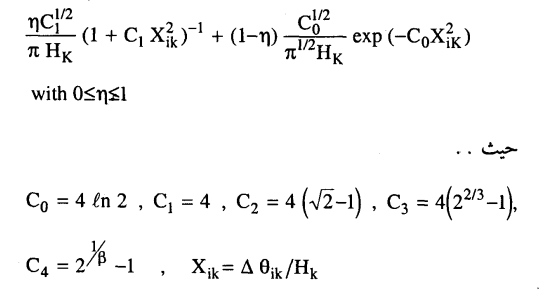
Hk هو العرض الكلي عند نصف ارتفاع القمة لانعكاس براج
(Full - width at half maximum (FWHM وهذا العرض (FWHM).
يكون عادة متغيرا مع زاوية التشتت حسب المعادلة ...

كذلك ...

أما بالنسبة للأشعة الخلفية back ground فإنه لا توجد طريقة معينة للتعامل معه فهو نتيجة لعدة مصادر هي
الحجب غير الكافي insufficient shielding
التشتت المنتشر diffuse scattering
التشتت غير الذاتي incoherent shielding
وهذه الاشعة الخلفية وتغيرها مع الزاوية غالبا ما تعرف بتدقيق متسلسلة في θ2 كالاتي:

حيث bn هي متغيرات خاضعة للتدقيق حسب المعادلة (1-11) والتوافق بين النموذج المفترض والبيانات العملية للحيود تقاس بالكميات الاتية:
1- لشكل الحيود الكمية Rp تعطى بالمعادلة ...

2- لشكل الحيود المزود بالأثقال Rwp (weighted) تعطى بالعلاقة ...

3- قيمة براج الكمية RB تعطى بالمعادلة ...
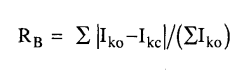
5- قيمة جودة المطابقة Goodness of fit)) التي يجب أن تقترب من الواحد الصحيح.
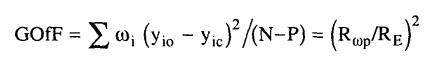
حيث N، P هما عدد النقاط في شكل الحيود وعدد المتغيرات التي يتم تدقيقها بالترتيب.
وأهم القيم السابق ذكرها هما قيمتي GOFF، Rwpحيث توضحان في المقام القيم التي يجري تصغيرها كذلك القيمة RB لها استخدام كبير حيث إنها تعتمد على مطابقة متغيرات التركيب أكثر من متغيرات شكل الحيود.
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


