إذا كانت الذرات في البلورات تتخذ مواقع تشكل شبيكة ثلاثية الأبعاد وتمتد لمسافات معقولة أي أن لها انتظاما بعيد المدى فإن السوائل والأجسام الأمورفية لا تتمتع إلا بانتظام قصير المدى.

ومعنى هذا أن أقرب الجيران لذرة ما قد تنتظم في ترتيب معين يشبه تقريبا ما يحدث في البلورات إلا أنه على بعد مسافة معينة من تلك الذرة يختفي الترتيب؛ لذلك فإن حيود الأشعة من السينية من السوائل يتخذ نمطا يتكون من حلقة واحدة أو عدة حلقات سميكة، وقد اصطلح على تسمية الحلقة الواحدة الهالة الأمورفية، وهي غالبا أعرض بكثير من الانعكاسات الناجمة عن حيود الأشعة السينية من بلورة أحادية وذلك بسبب تباين المسافات بين الذرات المختلفة في المواد الأمورفية.

وتعالج أنماط الحيود للأشعة السينية من المواد الأمورفية باستخدام فوتومتر لقياس شدة الأشعة بعد حيودها كدالة في زاوية الحيود. ثم تجري الحسابات بعد ذلك بطريقة التوزيع الشعاعي (القطري) وقد يكون الشكل (13-1) نموذجا لمنحني التوزيع القطري حيث يبدو تغير الكثافة مع المسافة المقاسة بالنسبة لذرة محددة، وتشير القمة الأولى بالمنحني إلى المسافة بين تلك الذرة وأقرب جيرانها، أما المساحة المحصورة أسفل تلك القمة فتتناسب عدد جيران الذرة المعنية.

أما القمة الثانية فهي أدنى وأكثر اتساعا من الأولى مما يدل على تلاشي النظام أو الترتيب سريعا إذا ما ابتعدنا عن الذرة المعنية وغالبا ما نلجأ إلى معادلة «براج» الشهيرة.

1.68  d sin θ  = λ

لتقدير المسافة بين أقرب الجيران بصورة تقريبية، حيث d هي المسافة المطلوبة، و θ الزاوية المناظرة لمنتصف الهالة الأمورفية.

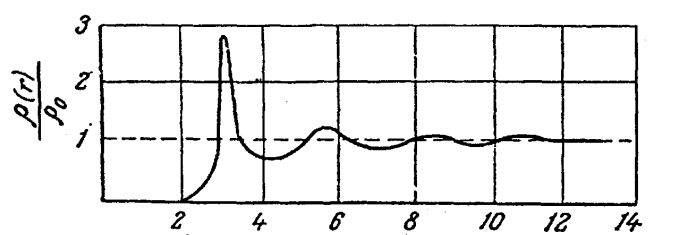
شكل (13-1)

منحني التوزيع القطري لذرات الزئبق السائل حيث (r)ρ هي الكثافة عند مسافة r من ذرة محددة، ₀ρ متوسط الكثافة داخل العينة.

مواضيع ذات صلة

تأثير تصغير مقاييس الحبيبات على خواص المادة

الحبيبات

غياب المثالية عن الترتيب الذري

الشبكات البلورية

الإشعاع السينكروتروني Synchrotron Radiation

مراكز الالوان Color Centers

الأشعة وحيدة الموجة في تجارب الحيود من البلورات

شاشات عرض البلورات السائلة ذات المصفوفات الفعالة: «AMLCD «Active Matrix Liquid Crystal Display

استخدام البلورات السائلة في أجهزة العرض

السلوك الكهروبصري لأغشية (PDLC)

الخواص الكهروبصرية لأغشية البلورات السائلة المنتشرة داخل بوليمر «PDLC»

الانكسار المزدوج وتأثره بالمجال الكهربائي Birefringence