
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الخواص الفيزيائية الأساسية للبلورات السائلة: الخواص العزلية Dielectric Properties
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص444–446
2023-10-11
1692
تعتبر السوائل العضوية النقية من المواد العازلة كهربيا وكذلك المواد الديامغناطيسية (σ ≈ 0). وتكون النفاذية المغناطيسية لها هيμ0 = 1 = 4 π X ≈ 1 أما معامل انكسارها فهو 1 = εμ n2 =
وعند الترددات المرتفعة تكون السماحية العزلية n2 = (ω → ∞) ε محكومة بمتوسط استقطابية ما يسمى بالتشوه الإلكتروني والأيوني للجزيء من خلال معادلة لورنتز - لورنتز:
حيث ρ هي كثافة المادة، m الوزن الجزيئي لها، NA عدد أقوجادرو أما <y> فهو متوسط الاستقطابية في وجود مجال كهربائي شدته E. أما عند الترددات المنخفضة فإن السماحية العزلية الإستاتيكية تعطى في أبسط صورها بمعادلة «کلاوزیوس – موسوتي:
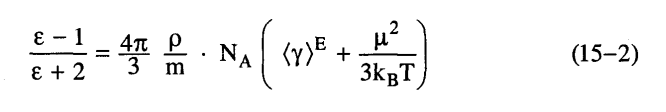
حيث  مقدار يعبر عن المركبة الاتجاهية لمتوسط الاستقطابية الإستاتيكية والتي تعتمد على عزم ثنائي القطب الكهربائي μ للجزيء.
مقدار يعبر عن المركبة الاتجاهية لمتوسط الاستقطابية الإستاتيكية والتي تعتمد على عزم ثنائي القطب الكهربائي μ للجزيء.
يوضح الشكل (15-8) كيفية تغير السماحية العزلية مع التردد في حالة سوائل ذات جزيئات قطبية (المنحني 1) وسوائل ذات جزيئات غير قطبية (المنحني 2). وتعتبر هذه المنحنيات أساسا لاستنتاج زمن الاسترخاء من معادلات «ديباي».

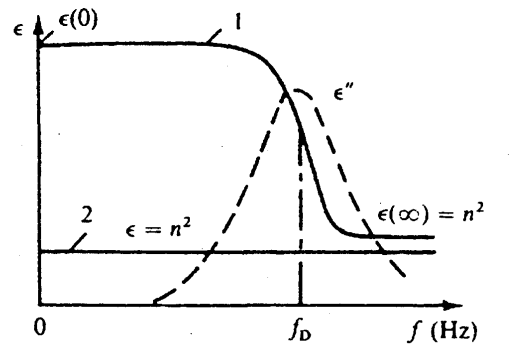
شكل (15-8)
تأثير التردد على السماحية العزلية للسوائل ذات الجزيئات القطبية (منحني 1) وغير القطبية (منحني 2). وترى أيضا العلاقة الخاصة بالفقد العزلي ''ε
حيث 'ε هو الشق الحقيقي، و''ε التخيلي للسماحية العزلية التخيلية، بحيث يشكلان معا السماحية المركبة.
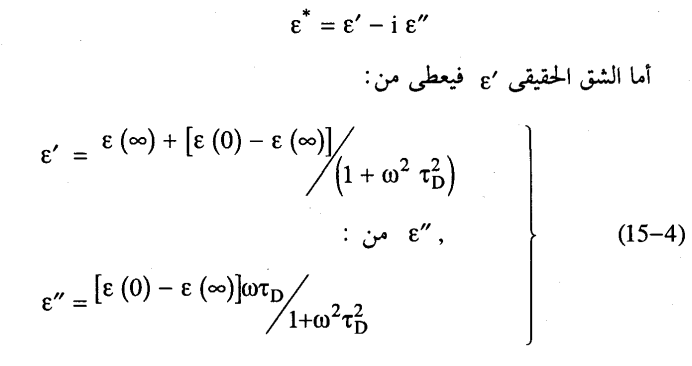
ذسوهكذا فالمعادلة (3-15) تصف المنحني الموضح بالشكل (15-8) الذي يمثل علاقة التردد بالشق الحقيقي من *ε والتردد المميز  كما يمثل علاقة التردد بالفقد العزلي. وهذا الفقد هو الذي يتسبب في وجود مركبة فعالة للتيار الكهربائي حتى في وسط عازل تماما لا يحتوي على ناقلات للشحنة والموصلية الكهربائية الناجمة عن الفقد العزلي هي:
كما يمثل علاقة التردد بالفقد العزلي. وهذا الفقد هو الذي يتسبب في وجود مركبة فعالة للتيار الكهربائي حتى في وسط عازل تماما لا يحتوي على ناقلات للشحنة والموصلية الكهربائية الناجمة عن الفقد العزلي هي:
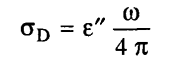
وفي الخلاصة فإن السماحية العزلية المركبة تصبح:

 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية
















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















