
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
قانون الجذب العام (نيوتن وثمرة التفاح)
المؤلف:
والتر لوين ووارن جولدستين
المصدر:
في حب الفيزياء
الجزء والصفحة:
ص64–65
2024-01-04
1979
يتحدث الناس في المعتاد عن قوانين نيوتن الثلاثة، لكن نيوتن في الواقع صاغ أربعة قوانين. وقد سمعنا جميعًا بقصة نيوتن عندما كان في بستان يراقب تفاحة تسقط من شجرة يزعم أحد المؤرخين السيرة نيوتن أن نيوتن نفسه من روى تلك الحكاية. وكتب ويليام ستوكلي صديق نيوتن مقتبسًا من محادثة جرت بين الاثنين قائلًا: «لقد استلهم الأمر برمته من سقوط ثمرة التفاح، حيث طرأ الأمر على ذهنه بينما كان يجلس متأملا، ففكر في نفسه لماذا يتحتم أن تسقط التفاحة على الأرض سقوطا عموديا» (1). لكن ما زال هناك كثيرون لا يصدقون هذه القصة. كما أن نيوتن لم يرو لستوكلي القصة إلا قبل وفاته بعام واحد ولم يذكرها مرة أخرى في مؤلفاته الضخام.
لكن رغم ذلك لا يجادل أحد في أن نيوتن كان أول من أدرك أن تلك القوة التي تسبب سقوط التفاحة من الشجرة هي ذاتها التي تحكم حركة القمر والأرض والشمس بل وجميع ما في الكون من أجسام. كانت تلك رؤية كاشفة فريدة؛ لكنه مرة أخرى لم يتوقف عند هذا الحد؛ فقد أدرك أن كل جسم في هذا الكون يجذب إليه كل جسم آخر، وخرج بمعادلة لحساب مدى قوة هذا الجذب، وهي المعادلة التي تعرف بقانونه للجذب العام. ينص هذا القانون على أن قوة الجذب التي بين جسمين تتناسب طرديا مع مجموع كتلتيهما، وتتناسب عكسيا مع مربع المسافة بينهما.
إذن، بعبارة أخرى، باستخدام مثال افتراضي تماما أؤكد على أنه لا علاقة بينه وبين الواقع، لو كان كوكبًا الأرض والمشتري يدوران حول الشمس من نفس المسافة، ولأن حجم كوكب المشتري يبلغ نحو 318 ضعفًا الحجم كوكب الأرض، لكانت قوة الجذب بين الشمس والمشتري ستعادل 318 مثل قوة الجذب بين الشمس والأرض. ولو كانت كتلتا الشمس والمشتري متساويتين، لكنّ المشتري في مساره الطبيعي الذي يبعد عن الشمس خمسة أمثال بعد مسار الأرض عن الشمس، حينها، ولأن قوة الجذب تتناسب تناسبا عكسيا مع مربع المسافة، ستبلغ قوة الجذب بين الشمس والأرض خمسة وعشرين مثل قوة الجذب بين الشمس والمشتري.
في كتاب نيوتن الشهير «المبادئ الرياضية للفلسفة الطبيعية»، الصادر عام 1678 – والذي نسميه اليوم «المبادئ» – لم يستعن نيوتن بمعادلة لتوضيح قانون الجذب العام، لكننا اعتدنا التعبير عنه في الفيزياء اليوم على النحو التالي:
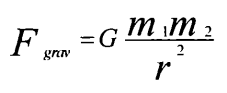
هنا، Fgrav هي قوة الجذب الثقالي بين جسم كتلته m1 وجسم آخر كتلته m2. وتعبر r عن المسافة بينهما؛ أما 2 فهي مربع المسافة. فماذا عن G؟ إنها ما يُطلق عليه ثابت الجاذبية. لقد علم نيوتن بالقطع بوجود هذا الثابت لكنه لم يذكره في كتاب المبادئ. ومن بين كثير من القياسات التي أجريت منذ ذلك الحين، صرنا الآن نعلم أن أدق قيمة لـ G هي 11–10 × 6.67428 ± 0.00067 (2) ونحن علماء الفيزياء، نعتقد أن هذه القيمة تنطبق على الكون بأسره مثلما خمن نيوتن.
لقد كان تأثير قوانين نيوتن مهولا، ولا يمكن أن يُوفَّى حقه من التقدير. كما أن كتاب المبادئ واحدٌ من أهم الكتب العلمية في التاريخ. فقوانينه تلك غيرت علمي الفيزياء والفلك بالكامل؛ فقد أتاحت حساب كتلة الشمس والكواكب، والطريقة التي يتم بها هذا الحساب بالغة الروعة. إذا عرفت الدورة المدارية لأي كوكب كان (كالمشتري أو الأرض مثلا) وعرفت المسافة التي تفصله عن الشمس، فحينها تستطيع أن تحسب كتلة الشمس. ألا يبدو ذلك كأنه سحر؟ بل إننا نستطيع أن نخطو خطوة إضافية إلى الأمام؛ حيث إننا إذا عرفنا الدورة المدارية لواحد من أقمار المشتري الساطعة (التي اكتشفها جاليليو عام 1609) وعرفنا المسافة بين المشتري وذلك القمر، نستطيع حينها أن نحسب كتلة المشتري. ومن ثم إذا عرفت الدورة المدارية لقمر الأرض الذي يدور حولها (27.32 يومًا) وعرفتَ متوسط المسافة بينه وبين الأرض (حوالي 239000 ميل) فستستطيع حينها حساب كتلة الأرض بقدر كبير من الدقة.
___________________________________________
هوامش
(1) نشرت الجمعية الملكية مؤخرًا صورة رقمية على الإنترنت لمخطوطة ستوكلي، تستطيع أن تطلع عليها على الموقع التالي http://royalsociety.org/turning–the–e–pages
(2) لو أردت استخدام هذه القيمة تأكد أن الكتل التي تقيسها بوحدة الكيلوجرام وأن المسافة بوحدة المتر. حينها يمكن قياس قوة الجاذبية بوحدة نيوتن.