
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Short distances
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 5
2024-01-29
1639
Now let’s think about smaller distances. Subdividing the meter is easy. Without much difficulty we can mark off one thousand equal spaces which add up to one meter. With somewhat more difficulty, but in a similar way (using a good microscope), we can mark off a thousand equal subdivisions of the millimeter to make a scale of microns (millionths of a meter). It is difficult to continue to smaller scales, because we cannot “see” objects smaller than the wavelength of visible light (about 5×10−7 meter).
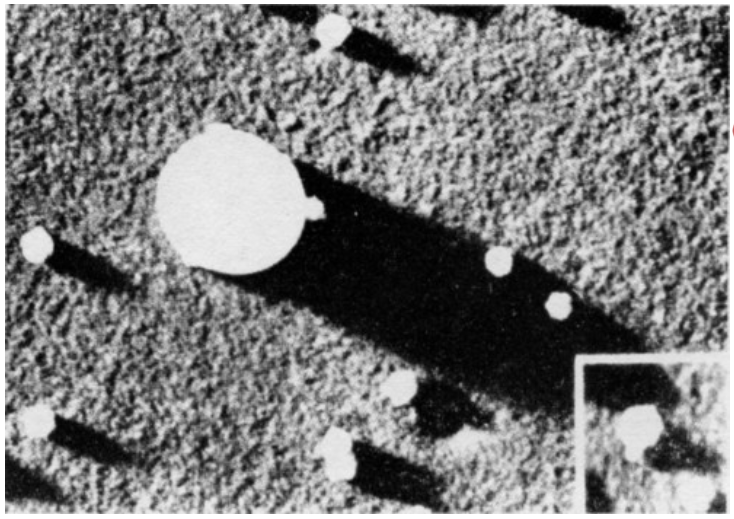
Fig. 5–9. Electron micrograph of some virus molecules. The “large” sphere is for calibration and is known to have a diameter of 2×10−7 meter (2000 Å).
We need not stop, however, at what we can see. With an electron microscope, we can continue the process by making photographs on a still smaller scale, say down to 10−8 meter (Fig. 5–9). By indirect measurements—by a kind of triangulation on a microscopic scale—we can continue to measure to smaller and smaller scales. First, from an observation of the way light of short wavelength (x-radiation) is reflected from a pattern of marks of known separation, we determine the wavelength of the light vibrations. Then, from the pattern of the scattering of the same light from a crystal, we can determine the relative location of the atoms in the crystal, obtaining results which agree with the atomic spacings also determined by chemical means. We find in this way that atoms have a diameter of about 10−10 meter.
There is a large “gap” in physical sizes between the typical atomic dimension of about 10−10 meter and the nuclear dimensions 10−15 meter, 10−5 times smaller. For nuclear sizes, a different way of measuring size becomes convenient. We measure the apparent area, σ, called the effective cross section. If we wish the radius, we can obtain it from σ=πr2, since nuclei are nearly spherical.
Measurement of a nuclear cross section can be made by passing a beam of high-energy particles through a thin slab of material and observing the number of particles which do not get through. These high-energy particles will plow right through the thin cloud of electrons and will be stopped or deflected only if they hit the concentrated weight of a nucleus. Suppose we have a piece of material 1 centimeter thick. There will be about 108 atomic layers. But the nuclei are so small that there is little chance that any nucleus will lie behind another. We might imagine that a highly magnified view of the situation—looking along the particle beam—would look like Fig. 5–10.

Fig. 5–10. Imagined view through a block of carbon 1 cm thick if only the nuclei were observed.
The chance that a very small particle will hit a nucleus on the trip through is just the total area covered by the profiles of the nuclei divided by the total area in the picture. Suppose that we know that in an area A of our slab of material there are N atoms (each with one nucleus, of course). Then the fraction of the area “covered” by the nuclei is Nσ/A. Now let the number of particles of our beam which arrive at the slab be n1 and the number which come out the other side be n2. The fraction which do not get through is (n1−n2)/n1, which should just equal the fraction of the area covered. We can obtain the radius of the nucleus from the equation 1
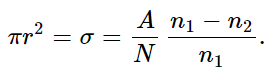
From such an experiment we find that the radii of the nuclei are from about 1 to 6 times 10−15 meter. The length unit 10−15 meter is called the fermi, in honor of Enrico Fermi (1901–1954).
What do we find if we go to smaller distances? Can we measure smaller distances? Such questions are not yet answerable. It has been suggested that the still unsolved mystery of nuclear forces may be unravelled only by some modification of our idea of space, or measurement, at such small distances.

It might be thought that it would be a good idea to use some natural length as our unit of length—say the radius of the earth or some fraction of it. The meter was originally intended to be such a unit and was defined to be (π/2) × 10−7 times the earth’s radius. It is neither convenient nor very accurate to determine the unit of length in this way. For a long time it has been agreed internationally that the meter would be defined as the distance between two scratches on a bar kept in a special laboratory in France. More recently, it has been realized that this definition is neither as precise as would be useful, nor as permanent or universal as one would like. It is currently being considered that a new definition be adopted, an agreed-upon (arbitrary) number of wavelengths of a chosen spectral line.
__________________________________
Measurements of distance and of time give results which depend on the observer. Two observers moving with respect to each other will not measure the same distances and times when measuring what appear to be the same things. Distances and time intervals have different magnitudes, depending on the coordinate system (or “frame of reference”) used for making the measurements. We shall study this subject in more detail in a later chapter.
Perfectly precise measurements of distances or times are not permitted by the laws of nature. We have mentioned earlier that the errors in a measurement of the position of an object must be at least as large as
Δx ≥ ℏ/2Δp,
where ℏ is a small fundamental physical constant called the reduced Planck constant and Δp is the error in our knowledge of the momentum (mass times velocity) of the object whose position we are measuring. It was also mentioned that the uncertainty in position measurements is related to the wave nature of particles.
The relativity of space and time implies that time measurements have also a minimum error, given in fact by
Δt ≥ ℏ/2ΔE,
where ΔE is the error in our knowledge of the energy of the process whose time period we are measuring. If we wish to know more precisely when something happened, we must know less about what happened, because our knowledge of the energy involved will be less. The time uncertainty is also related to the wave nature of matter.
_______________________________________________________
Margin
1- This equation is right only if the area covered by the nuclei is a small fraction of the total, i.e., if (n1−n2)/n1 is much less than 1. Otherwise, we must make a correction for the fact that some nuclei will be partly obscured by the nuclei in front of them.