
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Acceleration
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 8
2024-02-05
1263
The next step in developing the equations of motion is to introduce another idea which goes beyond the concept of velocity to that of change of velocity, and we now ask, “How does the velocity change?” In previous chapters we have discussed cases in which forces produce changes in velocity. You may have heard with great excitement about some car that can get from rest to 60 miles an hour in ten seconds flat. From such a performance we can see how fast the speed changes, but only on the average. What we shall now discuss is the next level of complexity, which is how fast the velocity is changing. In other words, by how many feet per second does the velocity change in a second, that is, how many feet per second, per second? We previously derived the formula for the velocity of a falling body as v=32t, which is charted in Table 8–4, and now we want to find out how much the velocity changes per second; this quantity is called the acceleration.
Acceleration is defined as the time rate of change of velocity. From the preceding discussion we know enough already to write the acceleration as the derivative dv/dt, in the same way that the velocity is the derivative of the distance. If we now differentiate the formula v=32t we obtain, for a falling body,

[To differentiate the term 32t we can utilize the result obtained in a previous problem, where we found that the derivative of Bt is simply B (a constant). So by letting B=32, we have at once that the derivative of 32t is 32.] This means that the velocity of a falling body is changing by 32 feet per second, per second always. We also see from Table 8–4 that the velocity increases by 32 ft/sec in each second. This is a very simple case, for accelerations are usually not constant. The reason the acceleration is constant here is that the force on the falling body is constant, and Newton’s law says that the acceleration is proportional to the force.
As a further example, let us find the acceleration in the problem we have already solved for the velocity. Starting with
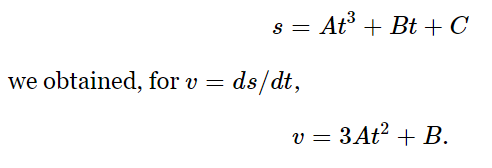
Since acceleration is the derivative of the velocity with respect to the time, we need to differentiate the last expression above. Recall the rule that the derivative of the two terms on the right equals the sum of the derivatives of the individual terms. To differentiate the first of these terms, instead of going through the fundamental process again we note that we have already differentiated a quadratic term when we differentiated 16t2, and the effect was to double the numerical coefficient and change the t2 to t; let us assume that the same thing will happen this time, and you can check the result yourself. The derivative of 3At2 will then be 6At. Next we differentiate B, a constant term; but by a rule stated previously, the derivative of B is zero; hence this term contributes nothing to the acceleration. The final result, therefore, is a= dv/dt= 6At.
For reference, we state two very useful formulas, which can be obtained by integration. If a body starts from rest and moves with a constant acceleration, g, its velocity v at any time t is given by

Various mathematical notations are used in writing derivatives. Since velocity is ds/dt and acceleration is the time derivative of the velocity, we can also write
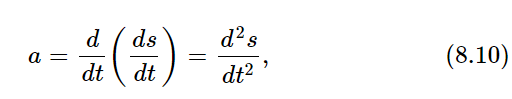
which are common ways of writing a second derivative.
We have another law that the velocity is equal to the integral of the acceleration. This is just the opposite of a=dv/dt; we have already seen that distance is the integral of the velocity, so distance can be found by twice integrating the acceleration.
In the foregoing discussion the motion was in only one dimension, and space permits only a brief discussion of motion in three dimensions. Consider a particle P which moves in three dimensions in any manner whatsoever. At the beginning of this chapter, we opened our discussion of the one-dimensional case of a moving car by observing the distance of the car from its starting point at various times. We then discussed velocity in terms of changes of these distances with time, and acceleration in terms of changes in velocity. We can treat three-dimensional motion analogously. It will be simpler to illustrate the motion on a two-dimensional diagram, and then extend the ideas to three dimensions. We establish a pair of axes at right angles to each other, and determine the position of the particle at any moment by measuring how far it is from each of the two axes. Thus each position is given in terms of an x-distance and a y-distance, and the motion can be described by constructing a table in which both these distances are given as functions of time. (Extension of this process to three dimensions requires only another axis, at right angles to the first two, and measuring a third distance, the z-distance. The distances are now measured from coordinate planes instead of lines.) Having constructed a table with x- and y-distances, how can we determine the velocity? We first find the components of velocity in each direction. The horizontal part of the velocity, or x-component, is the derivative of the x-distance with respect to the time, or

Now, given the components of velocity, how can we find the velocity along the actual path of motion? In the two-dimensional case, consider two successive positions of the particle, separated by a short distance Δs and a short time interval t2−t1=Δt. In the time Δt the particle moves horizontally a distance Δx ≈ vxΔt, and vertically a distance Δy ≈ vyΔt. (The symbol “≈” is read “is approximately.”) The actual distance moved is approximately
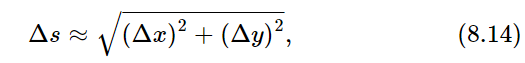
as shown in Fig. 8–3. The approximate velocity during this interval can be obtained by dividing by Δt and by letting Δt go to 0, as at the beginning of the chapter. We then get the velocity as
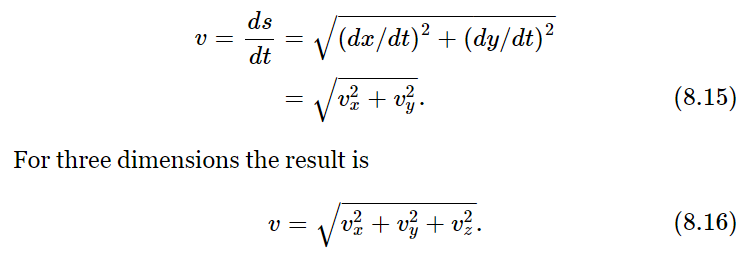
In the same way as we defined velocities, we can define accelerations: we have an x-component of acceleration ax, which is the derivative of vx, the x-component of the velocity (that is, ax=d2x/dt2, the second derivative of x with respect to t), and so on.
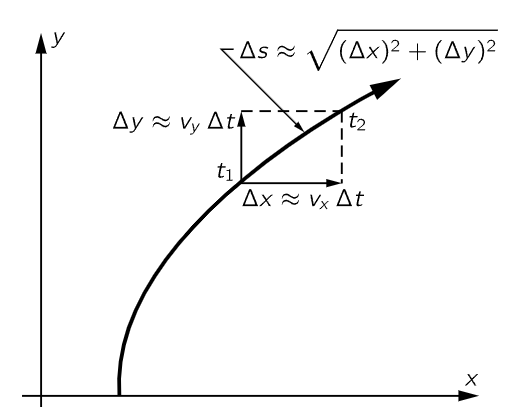
Fig. 8–3. Description of the motion of a body in two dimensions and the computation of its velocity.
Let us consider one nice example of compound motion in a plane. We shall take a motion in which a ball moves horizontally with a constant velocity u, and at the same time goes vertically downward with a constant acceleration −g; what is the motion? We can say dx/dt= vx= u. Since the velocity vx is constant,

and since the downward acceleration −g is constant, the distance y the object falls can be written as

What is the curve of its path, i.e., what is the relation between y and x? We can eliminate t from Eq. (8.18), since t=x/u. When we make this substitution, we find that

This relation between y and x may be considered as the equation of the path of the moving ball. When this equation is plotted we obtain a curve that is called a parabola; any freely falling body that is shot out in any direction will travel in a parabola, as shown in Fig. 8–4.
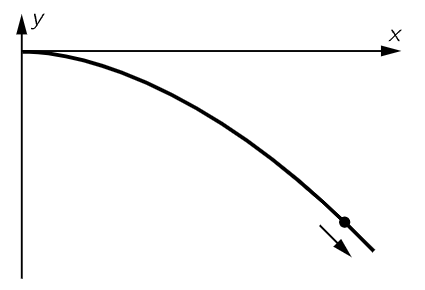
Fig. 8–4. The parabola described by a falling body with an initial horizontal velocity.