
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Four-vectors
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 15
2024-02-24
1846
Let us see what else we can discover in the Lorentz transformation. It is interesting to note that the transformation between the x’s and t’s is analogous in form to the transformation of the x’s and y’s for a rotation of coordinates. We then had

in which the new x′ mixes the old x and y, and the new y′ also mixes the old x and y; similarly, in the Lorentz transformation we find a new x′ which is a mixture of x and t, and a new t′ which is a mixture of t and x. So, the Lorentz transformation is analogous to a rotation, only it is a “rotation” in space and time, which appears to be a strange concept. A check of the analogy to rotation can be made by calculating the quantity
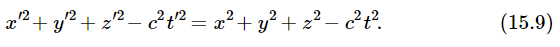
In this equation the first three terms on each side represent, in three-dimensional geometry, the square of the distance between a point and the origin (surface of a sphere) which remains unchanged (invariant) regardless of rotation of the coordinate axes. Similarly, Eq. (15.9) shows that there is a certain combination which includes time, that is invariant to a Lorentz transformation. Thus, the analogy to a rotation is complete, and is of such a kind that vectors, i.e., quantities involving “components” which transform the same way as the coordinates and time, are also useful in connection with relativity.
Thus, we contemplate an extension of the idea of vectors, which we have so far considered to have only space components, to include a time component. That is, we expect that there will be vectors with four components, three of which are like the components of an ordinary vector, and with these will be associated a fourth component, which is the analog of the time part.
This concept will be analyzed further in the next chapters, where we shall find that if the ideas of the preceding paragraph are applied to momentum, the transformation gives three space parts that are like ordinary momentum components, and a fourth component, the time part, which is the energy.
 الاكثر قراءة في مواضيع عامة في النظرية النسبية
الاكثر قراءة في مواضيع عامة في النظرية النسبية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















