
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The energy of an oscillator
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 24
2024-03-13
958
In a mechanical oscillator, how much kinetic energy is there? It is proportional to the square of the velocity. Now we come to an important point. Consider an arbitrary quantity A, which may be the velocity or something else that we want to discuss. When we write A=Ȃeiωt, a complex number, the true and honest A, in the physical world, is only the real part; therefore if, for some reason, we want to use the square of A, it is not right to square the complex number and then take the real part, because the real part of the square of a complex number is not just the square of the real part, but also involves the imaginary part. So, when we wish to find the energy, we have to get away from the complex notation for a while to see what the inner workings are.
Now the true physical A is the real part of A0 ei(ωt+Δ), that is, A=A0 cos(ωt+Δ), where Ȃ, the complex number, is written as A0 eiΔ. Now the square of this real physical quantity is A2=A20cos2 (ωt+Δ). The square of the quantity, then, goes up and down from a maximum to zero, like the square of the cosine. The square of the cosine has a maximum of 1 and a minimum of 0, and its average value is 1/2.
In many circumstances we are not interested in the energy at any specific moment during the oscillation; for a large number of applications, we merely want the average of A2, the mean of the square of A over a period of time large compared with the period of oscillation. In those circumstances, the average of the cosine squared may be used, so we have the following theorem: if A is represented by a complex number, then the mean of A2 is equal to 1/2 A20. Now A20 is the square of the magnitude of the complex Ȃ. (This can be written in many ways—some people like to write |Ȃ|2; others write, ȂȂ∗, Ȃ times its complex conjugate.) We shall use this theorem several times.
Now let us consider the energy in a forced oscillator. The equation for the forced oscillator is
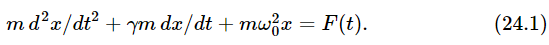
In our problem, of course, F(t) is a cosine function of t. Now let us analyze the situation: how much work is done by the outside force F? The work done by the force per second, i.e., the power, is the force times the velocity. (We know that the differential work in a time dt is Fdx, and the power is Fdx/dt.) Thus
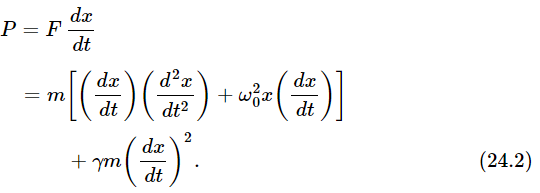
But the first two terms on the right can also be written as d/dt[1/2 m(dx/dt)2+1/2 mω20x2], as is immediately verified by differentiating. That is to say, the term in brackets is a pure derivative of two terms that are easy to understand—one is the kinetic energy of motion, and the other is the potential energy of the spring. Let us call this quantity the stored energy, that is, the energy stored in the oscillation. Suppose that we want the average power over many cycles when the oscillator is being forced and has been running for a long time. In the long run, the stored energy does not change—its derivative gives zero average effect. In other words, if we average the power in the long run, all the energy ultimately ends up in the resistive term γm(dx/dt)2. There is some energy stored in the oscillation, but that does not change with time, if we average over many cycles. Therefore the mean power ⟨P⟩ is

Using our method of writing complex numbers, and our theorem that ⟨A2⟩=1/2 A20, we may find this mean power. Thus, if 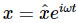 , then
, then 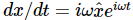 . Therefore, in these circumstances, the average power could be written as
. Therefore, in these circumstances, the average power could be written as

In the notation for electrical circuits, dx/dt is replaced by the current I (I is dq/dt, where q corresponds to x), and mγ corresponds to the resistance R. Thus the rate of the energy loss—the power used up by the forcing function—is the resistance in the circuit times the average square of the current:
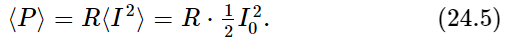
This energy, of course, goes into heating the resistor; it is sometimes called the heating loss or the Joule heating.
Another interesting feature to discuss is how much energy is stored. That is not the same as the power, because although power was at first used to store up some energy, after that the system keeps on absorbing power, insofar as there are any heating (resistive) losses. At any moment there is a certain amount of stored energy, so we would like to calculate the mean stored energy ⟨E⟩ also. We have already calculated what the average of (dx/dt)2 is, so we find

Now, when an oscillator is very efficient, and if ω is near ω0, so that 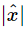 is large, the stored energy is very high—we can get a large stored energy from a relatively small force. The force does a great deal of work in getting the oscillation going, but then to keep it steady, all it has to do is to fight the friction. The oscillator can have a great deal of energy if the friction is very low, and even though it is oscillating strongly, not much energy is being lost. The efficiency of an oscillator can be measured by how much energy is stored, compared with how much work the force does per oscillation.
is large, the stored energy is very high—we can get a large stored energy from a relatively small force. The force does a great deal of work in getting the oscillation going, but then to keep it steady, all it has to do is to fight the friction. The oscillator can have a great deal of energy if the friction is very low, and even though it is oscillating strongly, not much energy is being lost. The efficiency of an oscillator can be measured by how much energy is stored, compared with how much work the force does per oscillation.
How does the stored energy compare with the amount of work that is done in one cycle? This is called the Q of the system, and Q is defined as 2π times the mean stored energy, divided by the work done per cycle. (If we were to say the work done per radian instead of per cycle, then the 2π disappears.)
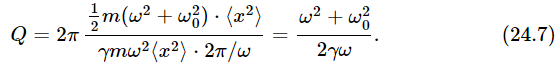
is not a very useful number unless it is very large. When it is relatively large, it gives a measure of how good the oscillator is. People have tried to define Q in the simplest and most useful way; various definitions differ a bit from one another, but if Q is very large, all definitions are in agreement. The most generally accepted definition is Eq. (24.7), which depends on ω. For a good oscillator, close to resonance, we can simplify (24.7) a little by setting ω=ω0, and we then have Q=ω0/γ, which is the definition of Q that we used before.
What is Q for an electrical circuit? To find out, we merely have to translate L for m, R for mγ, and 1/C for mω20 (see Table 23–1). The Q at resonance is Lω/R, where ω is the resonance frequency. If we consider a circuit with a high Q, that means that the amount of energy stored in the oscillation is very large compared with the amount of work done per cycle by the machinery that drives the oscillations.