The most dramatic moments in the development of physics are those in which great syntheses take place, where phenomena which previously had appeared to be different are suddenly discovered to be but different aspects of the same thing. The history of physics is the history of such syntheses, and the basis of the success of physical science is mainly that we are able to synthesize.
Perhaps the most dramatic moment in the development of physics during the 19th century occurred to J. C. Maxwell one day in the 1860s, when he combined the laws of electricity and magnetism with the laws of the behavior of light. As a result, the properties of light were partly unravelled—that old and subtle stuff that is so important and mysterious that it was felt necessary to arrange a special creation for it when writing Genesis. Maxwell could say, when he was finished with his discovery, “Let there be electricity and magnetism, and there is light!”
For this culminating moment there was a long preparation in the gradual discovery and unfolding of the laws of electricity and magnetism. This story we shall reserve for detailed study next year. However, the story is, briefly, as follows. The gradually discovered properties of electricity and magnetism, of electric forces of attraction and repulsion, and of magnetic forces, showed that although these forces were rather complex, they all fell off inversely as the square of the distance. We know, for example, that the simple Coulomb law for stationary charges is that the electric force field varies inversely as the square of the distance. As a consequence, for sufficiently great distances there is very little influence of one system of charges on another. Maxwell noted that the equations or the laws that had been discovered up to this time were mutually inconsistent when he tried to put them all together, and in order for the whole system to be consistent, he had to add another term to his equations. With this new term there came an amazing prediction, which was that a part of the electric and magnetic fields would fall off much more slowly with the distance than the inverse square, namely, inversely as the first power of the distance! And so, he realized that electric currents in one place can affect other charges far away, and he predicted the basic effects with which we are familiar today—radio transmission, radar, and so on.
It seems a miracle that someone talking in Europe can, with mere electrical influences, be heard thousands of miles away in Los Angeles. How is it possible? It is because the fields do not vary as the inverse square, but only inversely as the first power of the distance. Finally, then, even light itself was recognized to be electric and magnetic influences extending over vast distances, generated by an almost incredibly rapid oscillation of the electrons in the atoms. All these phenomena we summarize by the word radiation or, more specifically, electromagnetic radiation, there being one or two other kinds of radiation also. Almost always, radiation means electromagnetic radiation.
And thus is the universe knit together. The atomic motions of a distant star still have sufficient influence at this great distance to set the electrons in our eye in motion, and so we know about the stars. If this law did not exist, we would all be literally in the dark about the exterior world! And the electric surgings in a galaxy five billion light years away—which is the farthest object we have found so far—can still influence in a significant and detectable way the currents in the great “dish” in front of a radio telescope. And so it is that we see the stars and the galaxies.
This remarkable phenomenon is what we shall discuss in the present chapter. At the beginning of this course in physics we outlined a broad picture of the world, but we are now better prepared to understand some aspects of it, and so we shall now go over some parts of it again in greater detail. We begin by describing the position of physics at the end of the 19th century. All that was then known about the fundamental laws can be summarized as follows.
First, there were laws of forces: one force was the law of gravitation, which we have written down several times; the force on an object of mass m, due to another of mass M, is given by

where er is a unit vector directed from m to M, and r is the distance between them.
Next, the laws of electricity and magnetism, as known at the end of the 19th century, are these: the electrical forces acting on a charge q can be described by two fields, called E and B, and the velocity v of the charge q, by the equation
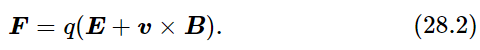
To complete this law, we have to say what the formulas for E and B are in a given circumstance: if a number of charges are present, E and the B are each the sum of contributions, one from each individual charge. So if we can find the E and B produced by a single charge, we need only to add all the effects from all the charges in the universe to get the total E and B! This is the principle of superposition.
What is the formula for the electric and magnetic field produced by one individual charge? It turns out that this is very complicated, and it takes a great deal of study and sophistication to appreciate it. But that is not the point. We write down the law now only to impress the reader with the beauty of nature, so to speak, i.e., that it is possible to summarize all the fundamental knowledge on one page, with notations that he is now familiar with. This law for the fields of an individual charge is complete and accurate, so far as we know (except for quantum mechanics) but it looks rather complicated. We shall not study all the pieces now; we only write it down to give an impression, to show that it can be written, and so that we can see ahead of time roughly what it looks like. As a matter of fact, the most useful way to write the correct laws of electricity and magnetism is not the way we shall now write them, but involves what are called field equations, which we shall learn about next year. But the mathematical notations for these are different and new, and so we write the law in an inconvenient form for calculation, but in notations that we now know.
The electric field, E, is given by
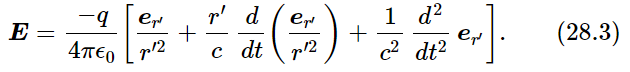
What do the various terms tell us? Take the first term, E=−qer′/4πϵ0r′2. That, of course, is Coulomb’s law, which we already know: q is the charge that is producing the field; er is the unit vector in the direction from the point P where E is measured, r is the distance from P to q. But, Coulomb’s law is wrong. The discoveries of the 19th century showed that influences cannot travel faster than a certain fundamental speed c, which we now call the speed of light. It is not correct that the first term is Coulomb’s law, not only because it is not possible to know where the charge is now and at what distance it is now, but also because the only thing that can affect the field at a given place and time is the behavior of the charges in the past. How far in the past? The time delay, or retarded time, so-called, is the time it takes, at speed c, to get from the charge to the field point P. The delay is r′/c.
So to allow for this time delay, we put a little prime on r, meaning how far away it was when the information now arriving at P left q. Just for a moment suppose that the charge carried a light, and that the light could only come to P at the speed c. Then when we look at q, we would not see where it is now, of course, but where it was at some earlier time. What appears in our formula is the apparent direction er′—the direction it used to be—the so-called retarded direction—and at the retarded distance r′. That would be easy enough to understand, too, but it is also wrong. The whole thing is much more complicated.
There are several more terms. The next term is as though nature were trying to allow for the fact that the effect is retarded, if we might put it very crudely. It suggests that we should calculate the delayed Coulomb field and add a correction to it, which is its rate of change times the time delay that we use. Nature seems to be attempting to guess what the field at the present time is going to be, by taking the rate of change and multiplying by the time that is delayed. But we are not yet through. There is a third term—the second derivative, with respect to t, of the unit vector in the direction of the charge. Now the formula is finished, and that is all there is to the electric field from an arbitrarily moving charge.
The magnetic field is given by

We have written these down only for the purpose of showing the beauty of nature or, in a way, the power of mathematics. We do not pretend to understand why it is possible to write so much in such a small space, but (28.3) and (28.4) contain the machinery by which electric generators work, how light operates, all the phenomena of electricity and magnetism. Of course, to complete the story we also need to know something about the behavior of the materials involved—the properties of matter—which are not described properly by (28.3).
To finish with our description of the world of the 19th century we must mention one other great synthesis which occurred in that century, one with which Maxwell had a great deal to do also, and that was the synthesis of the phenomena of heat and mechanics. We shall study that subject soon.
What had to be added in the 20th century was that the dynamical laws of Newton were found to be all wrong, and quantum mechanics had to be introduced to correct them. Newton’s laws are approximately valid when the scale of things is sufficiently large. These quantum-mechanical laws, combined with the laws of electricity, have only recently been combined to form a set of laws called quantum electrodynamics. In addition, there were discovered a number of new phenomena, of which the first was radioactivity, discovered by Becquerel in 1896—he just sneaked it in under the 19th century. This phenomenon of radioactivity was followed up to produce our knowledge of nuclei and new kinds of forces that are not gravitational and not electrical, but new particles with different interactions, a subject which has still not been unravelled.
For those purists who know more (the professors who happen to be reading this), we should add that when we say that (28.3) is a complete expression of the knowledge of electrodynamics, we are not being entirely accurate. There was a problem that was not quite solved at the end of the 19th century. When we try to calculate the field from all the charges including the charge itself that we want the field to act on, we get into trouble trying to find the distance, for example, of a charge from itself, and dividing something by that distance, which is zero. The problem of how to handle the part of this field which is generated by the very charge on which we want the field to act is not yet solved today. So we leave it there; we do not have a complete solution to that puzzle yet, and so we shall avoid the puzzle for as long as we can.
 الاكثر قراءة في الكهرومغناطيسية
الاكثر قراءة في الكهرومغناطيسية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


