
The momentum of light
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 34
الجزء والصفحة:
Volume I, Chapter 34
 2024-03-28
2024-03-28
 1901
1901
We have never said anything about the effects of the magnetic field that is associated with light. Ordinarily, the effects of the magnetic field are very small, but there is one interesting and important effect which is a consequence of the magnetic field. Suppose that light is coming from a source and is acting on a charge and driving that charge up and down. We will suppose that the electric field is in the x-direction, so the motion of the charge is also in the x-direction: it has a position x and a velocity v, as shown in Fig. 34–13. The magnetic field is at right angles to the electric field. Now as the electric field acts on the charge and moves it up and down, what does the magnetic field do? The magnetic field acts on the charge (say an electron) only when it is moving; but the electron is moving, it is driven by the electric field, so the two of them work together: While the thing is going up and down it has a velocity and there is a force on it, B times v times q; but in which direction is this force? It is in the direction of the propagation of light. Therefore, when light is shining on a charge and it is oscillating in response to that light, there is a driving force in the direction of the light beam. This is called radiation pressure or light pressure.
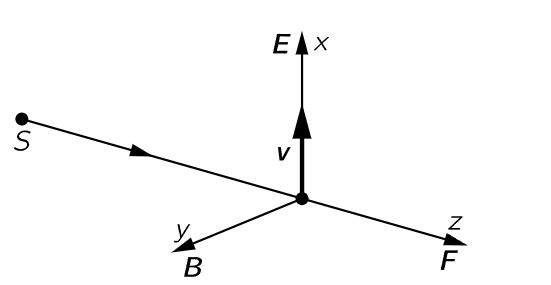
Fig. 34–13. The magnetic force on a charge which is driven by the electric field is in the direction of the light beam.
Let us determine how strong the radiation pressure is. Evidently it is F=qvB or, since everything is oscillating, it is the time average of this, ⟨F⟩.
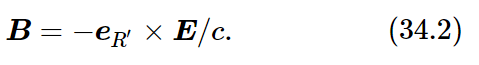
From (34.2) the strength of the magnetic field is the same as the strength of the electric field divided by c, so we need to find the average of the electric field, times the velocity, times the charge, times 1/c: ⟨F⟩=q⟨vE⟩/c. But the charge q times the field E is the electric force on a charge, and the force on the charge times the velocity is the work dW/dt being done on the charge! Therefore, the force, the “pushing momentum,” that is delivered per second by the light, is equal to 1/c times the energy absorbed from the light per second! That is a general rule, since we did not say how strong the oscillator was, or whether some of the charges cancel out. In any circumstance where light is being absorbed, there is a pressure. The momentum that the light delivers is always equal to the energy that is absorbed, divided by c:

That light carries energy we already know. We now understand that it also carries momentum, and further, that the momentum carried is always 1/c times the energy.
When light is emitted from a source there is a recoil effect: the same thing in reverse. If an atom is emitting an energy W in some direction, then there is a recoil momentum p=W/c. If light is reflected normally from a mirror, we get twice the force.
That is as far as we shall go using the classical theory of light. Of course, we know that there is a quantum theory, and that in many respects light acts like a particle. The energy of a light-particle is a constant times the frequency:

We now appreciate that light also carries a momentum equal to the energy divided by c, so it is also true that these effective particles, these photons, carry a momentum
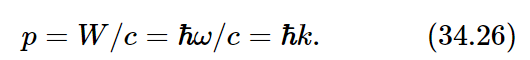
The direction of the momentum is, of course, the direction of propagation of the light. So, to put it in vector form,

We also know, of course, that the energy and momentum of a particle should form a four-vector. We have just discovered that ω and k form a four-vector. Therefore, it is a good thing that (34.27) has the same constant in both cases; it means that the quantum theory and the theory of relativity are mutually consistent.
Equation (34.27) can be written more elegantly as pμ=ℏkμ, a relativistic equation, for a particle associated with a wave. Although we have discussed this only for photons, for which k (the magnitude of k) equals ω/c and p=W/c, the relation is much more general. In quantum mechanics all particles, not only photons, exhibit wavelike properties, but the frequency and wave number of the waves is related to the energy and momentum of particles by (34.27) (called the de Broglie relations) even when p is not equal to W/c.
A beam of right or left circularly polarized light also carries angular momentum in an amount proportional to the energy E of the wave. In the quantum picture, a beam of circularly polarized light is regarded as a stream of photons, each carrying an angular momentum ±ℏ, along the direction of propagation. That is what becomes of polarization in the corpuscular point of view—the photons carry angular momentum like spinning rifle bullets.
 الاكثر قراءة في الضوء
الاكثر قراءة في الضوء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


