
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Thermionic emission
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 42
2024-06-03
1745
We may give another example of a very practical situation that is similar to the evaporation of a liquid—so similar that it is not worth making a separate analysis. It is essentially the same problem. In a radio tube there is a source of electrons, namely a heated tungsten filament, and a positively charged plate to attract the electrons. Any electron that escapes from the surface of the tungsten is immediately swept away to the plate. That is our ideal “pump,” which is “pumping” the electrons away all the time. Now the question is: How many electrons per second can we get out of a piece of tungsten, and how does that number vary with temperature? The answer to that problem is the same as (42.5), because it turns out that in a piece of metal, electrons are attracted to the ions, or to atoms, of the metal. They are attracted, if we may say it crudely, to the metal. In order to get an electron out of a piece of metal, it takes a certain amount of energy or work to pull it out. This work varies with the different kinds of metal. In fact, it varies even with the character of the surface of a given kind of metal, but the total work may be a few electron volts, which, incidentally, is typical of the energy involved in chemical reactions. We can remember the latter fact by remembering that the voltage in a chemical cell like a flashlight battery, which is produced by chemical reactions, is about one volt.
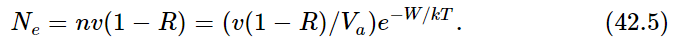
How can we find out how many electrons come out per second? It would be quite difficult to analyze the effects on the electrons going out; it is easier to analyze the situation the other way. So, we could start out by imagining that we did not draw the electrons away, and that the electrons were like a gas, and could come back to the metal. Then there would be a certain density of electrons at equilibrium which would, of course, be given by exactly the same formula as (42.1), where Va is the volume per electron in the metal, roughly, and W is equal to qeϕ, where ϕ is the so-called work function, or the voltage needed to pull an electron off the surface. This would tell us how many electrons would have to be in the surrounding space and striking the metal in order to balance the ones that are coming out.

And thus, it is easy to calculate how many are coming out if we sweep away all of them, because the number that are coming out is exactly equal to the number that would be going in with the above density of electron “vapor.” In other words, the answer is that the current of electricity that comes in per unit area is equal to the charge on each times the number that arrive per second per unit area, which is the number per unit volume times the velocity, as we have seen many times:
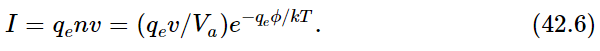
Now one electron volt corresponds to kT at a temperature of 11,600 degrees. The filament of the tube may be operating at a temperature of, say, 1100 degrees, so the exponential factor is something like e−10; when we change the temperature a little bit, the exponential factor changes a lot. Thus, again, the central feature of the formula is the e−qeϕ/kT. As a matter of fact, the factor in front is quite wrong—it turns out that the behavior of electrons in a metal is not correctly described by the classical theory, but by quantum mechanics, but this only changes the factor in front a little. Actually, no one has ever been able to get the thing straightened out very well, even though many people have used the high-class quantum-mechanical theory for their calculations. The big problem is, does W change slightly with temperature? If it does, one cannot distinguish a W changing slowly with temperature from a different coefficient in front. That is, if W changed linearly, say, with temperature, so that W=W0+αkT, then we would have
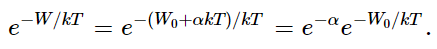
Thus a linearly temperature-dependent W is equivalent to a shifted “constant.” It is really quite difficult and usually fruitless to try to obtain the coefficient in the front accurately.
 الاكثر قراءة في الديناميكا الحرارية
الاكثر قراءة في الديناميكا الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















