
Thermal ionization
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 42
الجزء والصفحة:
Volume I, Chapter 42
 2024-06-05
2024-06-05
 1616
1616
Now we go on to another example of the same idea; always the same idea. This has to do with ionization. Suppose that in a gas we have a whole lot of atoms which are in the neutral state, say, but the gas is hot and the atoms can become ionized. We would like to know how many ions there are in a given circumstance if we have a certain density of atoms per unit volume at a certain temperature. Again, we consider a box in which there are N atoms which can hold electrons. (If an electron has come off an atom, it is called an ion, and if the atom is neutral, we simply call it an atom.) Then suppose that, at any given moment, the number of neutral atoms is na, the number of ions is ni, and the number of electrons is ne, all per unit volume. The problem is: What is the relationship of these three numbers?
In the first place, we have two conditions or constraints on the numbers. For instance, as we very different conditions, like the temperature and so on, na+ni would remain constant, because this would be simply the number N of atomic nuclei that are in the box. If we keep the number of nuclei per unit volume fixed, and change, say, the temperature, then as the ionization proceeded some atoms would turn to ions, but the total number of atoms plus ions would be unchanged. That is, na+ni=N. Another condition is that if the entire gas is to be electrically neutral (and if we neglect double or triple ionization), that means that the number of ions is equal to the number of electrons at all times, or ni=ne. These are subsidiary equations that simply express the conservation of charge and the conservation of atoms.
These equations are true, and we ultimately will use them when we consider a real problem. But we want to obtain another relationship between the quantities. We can do this as follows. We again use the idea that it takes a certain amount of energy to lift the electron out of the atom, which we call the ionization energy, and we would write it as W, in order to make all of the formulas look the same. So, we let W equal the energy needed to pull an electron out of an atom and make an ion. Now we again say that the number of free electrons per unit volume in the “vapor” is equal to the number of bound electrons per unit volume in the atoms, times e to the minus the energy difference between being bound and being free, over kT. That is the basic equation again. How can we write it? The number of free electrons per unit volume would, of course, be ne, because that is the definition of ne. Now what about the number of electrons per unit volume that are bound to atoms? The total number of places that we could put the electrons is apparently na+ni, and we will suppose that when they are bound each one is bound within a certain volume Va. So the total amount of volume which is available to electrons which would be bound is (na+ni) Va, so we might want to write our formula as
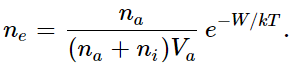
The formula is wrong, however, in one essential feature, which is the following: when an electron is already on an atom, another electron cannot come to that volume anymore! In other words, all the volumes of all the possible sites are not really available for the one electron which is trying to make up its mind whether or not to be in the vapor or in the condensed position, because in this problem there is an extra feature that when one electron is where another electron is, it is not allowed to go—it is repelled. For that reason, it comes out that we should count only that part of the volume which is available for an electron to sit on or not. That is, those which are already occupied do not count in the total available volume, but the only volume which is allowed is that of the ions, where there are vacant places for the electron to go. Then, in those circumstances, we find that a nicer way to write our formula is

This formula is called the Saha ionization equation. Now let us see if we can understand qualitatively why a formula like this is right, by arguing about the kinetic things that are happening.
First, every once in a while an electron comes to an ion and they combine to make an atom. And also, every once in a while, an atom gets into a collision and breaks up into an ion and an electron. Now those two rates must be equal. How fast do electrons and ions find each other? The rate is certainly increased if the number of electrons per unit volume is increased. It is also increased if the number of ions per unit volume is increased. That is, the total rate at which recombination is occurring is certainly proportional to the number of electrons times the number of ions. Now the total rate at which ionization is occurring due to collisions must be dependent linearly on how many atoms there are to ionize. And so, the rates will balance when there is some relationship between the product neni and the number of atoms, na. The fact that this relationship happens to be given by this particular formula, where W is the ionization energy, is of course a little bit more information, but we can easily understand that the formula would necessarily involve the concentrations of the electrons, ions, and atoms in the combination neni/na to produce a constant independent of the n’s, and dependent only on temperature, the atomic cross sections, and other constant factors.
We may also note that, since the equation involves the numbers per unit volume, if we were to do two experiments with a given total number N of atoms plus ions, that is, a certain fixed number of nuclei, but using boxes with different volumes, the n’s would all be smaller in the larger box. But since the ratio neni/na stays the same, the total number of electrons and ions must be greater in the larger box. To see this, suppose that there are N nuclei inside a box of volume V, and that a fraction f of them is ionized. Then ne= fN/V= ni, and na=(1−f) N/V. Then our equation becomes

In other words, if we take a smaller and smaller density of atoms, or make the volume of the container bigger and bigger, the fraction f of electrons and ions must increase. That ionization, just from “expansion” as the density goes down, is the reason why we believe that at very low densities, such as in the cold space between the stars, there may be ions present, even though we might not understand it from the point of view of the available energy. Although it takes many, many kT of energy to make them, there are ions present.
Why can there be ions present when there is so much space around, while if we increase the density, the ions tend to disappear? Answer: Consider an atom. Every once in a while, light, or another atom, or an ion, or whatever it is that maintains thermal equilibrium, strikes it. Very rarely, because it takes such a terrific amount of excess energy, an electron comes off and an ion is left. Now that electron, if the space is enormous, wanders and wanders and does not come near anything for years, perhaps. But once in a very great while, it does come back to an ion and they combine to make an atom. So, the rate at which electrons are coming out from the atoms is very slow. But if the volume is enormous, an electron which has escaped takes so long to find another ion to recombine with that its probability of recombination is very, very small; thus, in spite of the large excess energy needed, there may be a reasonable number of electrons.
 الاكثر قراءة في الديناميكا الحرارية
الاكثر قراءة في الديناميكا الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


