Thermodynamics is a rather difficult and complex subject when we come to apply it, and it is not appropriate for us to go very far into the applications in this course. The subject is of very great importance, of course, to engineers and chemists, and those who are interested in the subject can learn about the applications in physical chemistry or in engineering thermodynamics. There are also good equation reference books, such as Zemansky’s Heat and Thermodynamics, where one can learn more about the subject. In the Encyclopedia Britannica, fourteenth edition, one can find excellent articles on thermodynamics and thermochemistry, and in the article on chemistry, the sections on physical chemistry, vaporization, liquefication of gases, and so on.
The subject of thermodynamics is complicated because there are so many different ways of describing the same thing. If we wish to describe the behavior of a gas, we can say that the pressure depends on the temperature and on the volume, or we can say that the volume depends on the temperature and the pressure. Or with respect to the internal energy U, we might say that it depends on the temperature and volume, if those are the variables we have chosen—but we might also say that it depends on the temperature and the pressure, or the pressure and the volume, and so on. In the last chapter we discussed another function of temperature and volume, called the entropy S, and we can of course construct as many other functions of these variables as we like: U−TS is a function of temperature and volume. So we have a large number of different quantities which can be functions of many different combinations of variables.
To keep the subject simple in this chapter, we shall decide at the start to use temperature and volume as the independent variables. Chemists use temperature and pressure, because they are easier to measure and control in chemical experiments, but we shall use temperature and volume throughout this chapter, except in one place where we shall see how to make the transformation into the chemists’ system of variables.
We shall first, then, consider only one system of independent variables: temperature and volume. Secondly, we shall discuss only two dependent functions: the internal energy and the pressure. All the other functions can be derived from these, so it is not necessary to discuss them. With these limitations, thermodynamics is still a fairly difficult subject, but it is not quite so impossible!
First we shall review some mathematics. If a quantity is a function of two variables, the idea of the derivative of the quantity requires a little more careful thought than for the case where there is only one variable. What do we mean by the derivative of the pressure with respect to the temperature? The pressure change accompanying a change in the temperature depends partly, of course, on what happens to the volume while T is changing. We must specify the change in V before the concept of a derivative with respect to T has a precise meaning. We might ask, for example, for the rate of change of P with respect to T if V is held constant. This ratio is just the ordinary derivative that we usually write as dP/dT. We customarily use a special symbol, ∂P/∂T, to remind us that P depends on another variable V as well as on T, and that this other variable is held constant. We shall not only use the symbol ∂ to call attention to the fact that the other variable is held constant, but we shall also write the variable that is held constant as a subscript, (∂P/∂T)V. Since we have only two independent variables, this notation is redundant, but it will help us keep our wits about us in the thermodynamic jungle of partial derivatives.
Let us suppose that the function f(x,y) depends on the two independent variables x and y. By (∂f/∂x)y we mean simply the ordinary derivative, obtained in the usual way, if we treat y as a constant:
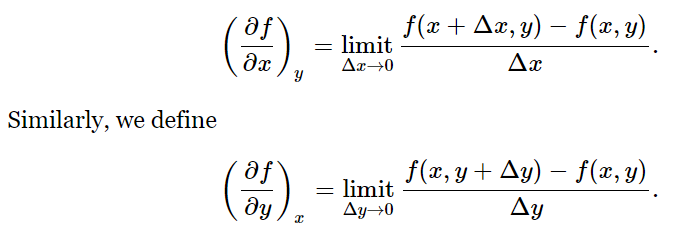
For example, if f(x,y)=x2+yx, then (∂f/∂x)y=2x+y, and (∂f/∂y)x=x. We can extend this idea to higher derivatives: ∂2f/∂y2 or ∂2f/∂y∂x. The latter symbol indicates that we first differentiate f with respect to x, treating y as a constant, then differentiate the result with respect to y, treating x as a constant. The actual order of differentiation is immaterial: ∂2f/∂x∂y=∂2f/∂y∂x.
We will need to compute the change Δf in f(x,y) when x changes to x+Δx and y changes to y+Δy. We assume throughout the following that Δx and Δy are infinitesimally small:
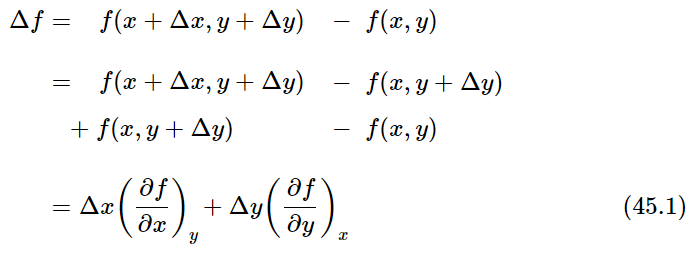
The last equation is the fundamental relation that expresses Δf in terms of Δx and Δy.
As an example of the use of this relation, let us calculate the change in the internal energy U(T,V) when the temperature changes from T to T+ΔT and the volume changes from V to V+ΔV. Using Eq. (45.1), we write
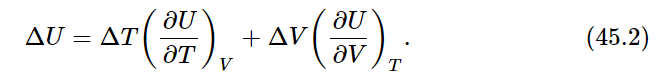
In our last chapter we found another expression for the change ΔU in the internal energy when a quantity of heat ΔQ was added to the gas:

In comparing Eqs. (45.2) and (45.3) one might at first be inclined to think that P=−(∂U/∂V)T, but this is not correct. To obtain the correct relation, let us first suppose that we add a quantity of heat ΔQ to the gas while keeping the volume constant, so that ΔV=0. With ΔV=0, Eq. (45.3) tells us that ΔU=ΔQ, and Eq. (45.2) tells us that ΔU=(∂U/∂T)VΔT, so that (∂U/∂T)V=ΔQ/ΔT. The ratio ΔQ/ΔT, the amount of heat one must put into a substance in order to change its temperature by one degree with the volume held constant, is called the specific heat at constant volume and is designated by the symbol CV. By this argument we have shown that

Now let us again add a quantity of heat ΔQ to the gas, but this time we will hold T constant and allow the volume to change by ΔV. The analysis in this case is more complex, but we can calculate ΔU by the argument of Carnot.
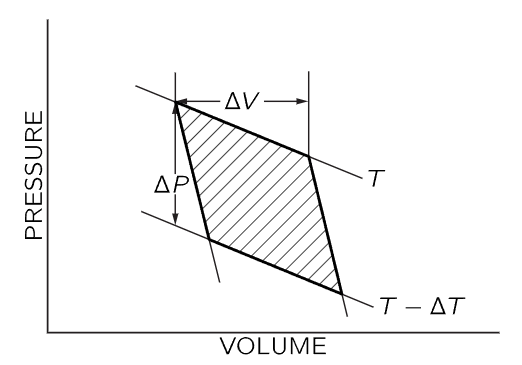
Fig. 45–1. Pressure-volume diagram for a Carnot cycle. The curves marked T and T−ΔT are isothermal lines; the steeper curves are adiabatic lines. ΔV is the volume change as heat ΔQ is added to the gas at constant temperature T. ΔP is the pressure change at constant volume as the gas temperature is changed from T to T−ΔT.
The pressure-volume diagram for the Carnot cycle is shown in Fig. 45–1. As we have already shown, the total amount of work done by the gas in a reversible cycle is ΔQ(ΔT/T), where ΔQ is the amount of heat energy added to the gas as it expands isothermally at temperature T from volume V to V+ΔV, and T−ΔT is the final temperature reached by the gas as it expands adiabatically on the second leg of the cycle. Now we will show that this work done is also given by the shaded area in Fig. 45–1. In any circumstances, the work done by the gas is ∫PdV, and is positive when the gas expands and negative when the gas is compressed. If we plot P vs. V, the variation of P and V is represented by a curve which gives the value of P corresponding to a particular value of V. As the volume changes from one value to another, the work done by the gas, the integral ∫PdV, is the area under the curve connecting the initial and final values of V. When we apply this idea to the Carnot cycle, we see that as we go around the cycle, paying attention to the sign of the work done by the gas, the net work done by the gas is just the shaded area in Fig. 45–1.
Now we want to evaluate the shaded area geometrically. The cycle we have used in Fig. 45–1 differs from that used in the previous chapter in that we now suppose that ΔT and ΔQ are infinitesimally small. We are working between adiabatic lines and isothermal lines that are very close together, and the figure described by the heavy lines in Fig. 45–1 will approach a parallelogram as the increments ΔT and ΔQ approach zero. The area of this parallelogram is just ΔVΔP, where ΔV is the change in volume as energy ΔQ is added to the gas at constant temperature, and ΔP is the change in pressure as the temperature changes by ΔT at constant volume. One can easily show that the shaded area in Fig. 45–1 is given by ΔVΔP by recognizing that the shaded area is equal to the area enclosed by the dotted lines in Fig. 45–2, which in turn differs from the rectangle bounded by ΔP and ΔV only by the addition and subtraction of the equal triangular areas in Fig. 45–2.
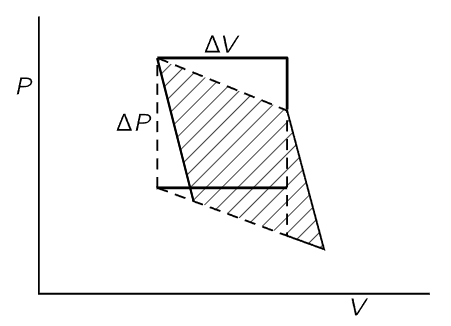
Fig. 45–2. Shaded area = area enclosed by dashed lines = area of rectangle = ΔPΔV.
Now let us summarize the results of the arguments we have developed so far:

Equation (45.5) expresses the essential result of Carnot’s argument. The whole of thermodynamics can be deduced from Eq. (45.5) and the First Law, which is stated in Eq. (45.3). Equation (45.5) is essentially the Second Law, although it was originally deduced by Carnot in a slightly different form, since he did not use our definition of temperature.
Now we can proceed to calculate (∂U/∂V)T. By how much would the internal energy U change if we changed the volume by ΔV? First, U changes because heat is put in, and second, U changes because work is done. The heat put in is
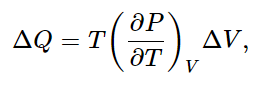
according to Eq. (45.5), and the work done on the substance is −PΔV. Therefore, the change ΔU in internal energy has two pieces:
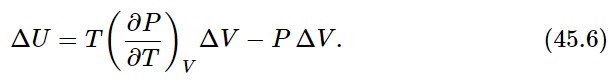
Dividing both sides by ΔV, we find for the rate of change of U with V at constant T
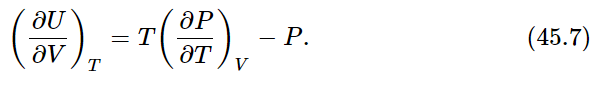
In our thermodynamics, in which T and V are the only variables and P and U are the only functions, Eqs. (45.3) and (45.7) are the basic equations from which all the results of the subject can be deduced.
 الاكثر قراءة في الديناميكا الحرارية
الاكثر قراءة في الديناميكا الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


