
The Fourier series
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 50
الجزء والصفحة:
Volume I, Chapter 50
 2024-06-29
2024-06-29
 1371
1371
A string has various natural modes of oscillation, and that any particular kind of vibration that may be set up by the starting conditions can be thought of as a combination—in suitable proportions—of several of the natural modes, oscillating together. For a string we found that the normal modes of oscillation had the frequencies ω0, 2ω0, 3ω0, … The most general motion of a plucked string, therefore, is composed of the sum of a sinusoidal oscillation at the fundamental frequency ω0, another at the second harmonic frequency 2ω0, another at the third harmonic 3ω0, etc. Now the fundamental mode repeats itself every period T1=2π/ω0. The second harmonic mode repeats itself every T2=2π/2ω0. It also repeats itself every T1=2T2, after two of its periods. Similarly, the third harmonic mode repeats itself after a time T1 which is 3 of its periods. We see again why a plucked string repeats its whole pattern with a periodicity of T1. It produces a musical tone.
We have been talking about the motion of the string. But the sound, which is the motion of the air, is produced by the motion of the string, so its vibrations too must be composed of the same harmonics—though we are no longer thinking about the normal modes of the air. Also, the relative strength of the harmonics may be different in the air than in the string, particularly if the string is “coupled” to the air via a sounding board. The efficiency of the coupling to the air is different for different harmonics.
If we let f(t) represent the air pressure as a function of time for a musical tone [such as that in Fig. 50–1(b)], then we expect that f(t) can be written as the sum of a number of simple harmonic functions of time—like cos ωt—for each of the various harmonic frequencies. If the period of the vibration is T, the fundamental angular frequency will be ω=2π/T, and the harmonics will be 2ω, 3ω, etc.
There is one slight complication. For each frequency we may expect that the starting phases will not necessarily be the same for all frequencies. We should, therefore, use functions like cos(ωt+ϕ). It is, however, simpler to use instead both the sine and cosine functions for each frequency. We recall that
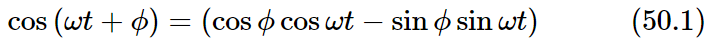
and since ϕ is a constant, any sinusoidal oscillation at the frequency ω can be written as the sum of a term with cos ωt and another term with sin ωt.
We conclude, then, that any function f(t) that is periodic with the period T can be written mathematically as
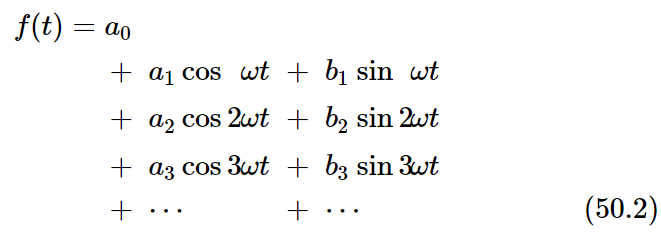
where ω=2π/T and the a’s and b’s are numerical constants which tell us how much of each component oscillation is present in the oscillation f(t). We have added the “zero-frequency” term a0 so that our formula will be completely general, although it is usually zero for a musical tone. It represents a shift of the average value (that is, the “zero” level) of the sound pressure. With it our formula can take care of any case. The equality of Eq. (50.2) is represented schematically in Fig. 50–2. (The amplitudes, an and bn, of the harmonic functions must be suitably chosen. They are shown schematically and without any particular scale in the figure.) The series (50.2) is called the Fourier series for f(t).
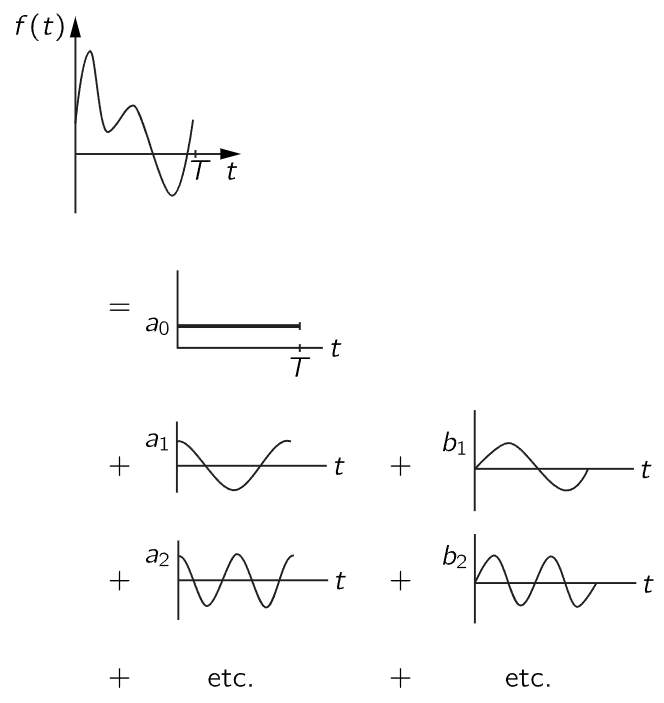
Fig. 50–2. Any periodic function f(t) is equal to a sum of simple harmonic functions.
We have said that any periodic function can be made up in this way. We should correct that and say that any sound wave, or any function we ordinarily encounter in physics, can be made up of such a sum. The mathematicians can invent functions which cannot be made up of simple harmonic functions—for instance, a function that has a “reverse twist” so that it has two values for some values of t! We need not worry about such functions here.
 الاكثر قراءة في الصوت
الاكثر قراءة في الصوت
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


