
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الأطر المرجعية القصورية
المؤلف:
ديفيد والاس
المصدر:
فلسفة علم الفيزياء
الجزء والصفحة:
ص36 – ص39
2024-07-29
786
«يبدو» أننا قد نتفق على ما يلي:
(1) نحتاج إلى طرح فكرة المكان المطلق لتوفير «إطار سكون» يمكن تعريف الحركات المستخدمة في قوانين نيوتن بالنسبة إليه (أو نحن نحتاج إلى إطار السكون نفسه على أي حال، ولا يمكن الاستغناء عنه بأي إطار تحدّده بعض الأجسام المادية). (2) يستحيل اكتشاف ما إذا كان الجسم في حالة سكون أم في حالة حركة منتظمة.
تبدو العبارتان السابقتان متناقضتين. ذلك أنه إذا لم يكن بإمكاننا اكتشاف الحركة بالنسبة إلى المكان المطلق، حتى ولو بطريقة غير مباشرة، فكيف تكون هذه الفكرة ضرورية للفيزياء؟ لكي ندرك أنه لا يوجد تناقض حقيقي، سنعرف الإطار المرجعي القصوري (أو لنسمه الإطار القصوري اختصارًا) بأنه أي إطار مرجعي يتحرك بسرعة متجهة ثابتة قياسًا بإطار السكون؛ أي بالمكان المطلق وفقًا لنيوتن. أو الأجسام الساكنة بالنسبة إلى إطار قصوري تتحرك بالقصور الذاتي – بمعنى أنها تتحرك في خط مستقيم وبسرعة ثابتة – طبقًا لإطار السكون وطبقًا إلى أي إطار قصوري آخر بالطبع.
والآن يتمثل مبدأ النسبية في أنه يمكن ممارسة الفيزياء، باستخدام معيار الحركة الذي يحدده أي إطار قصوري، ولا يلزم أن يكون ذلك الإطار هو إطار السكون. ويمكننا بالفعل أن نرى هذا (بدرجة كبيرة) بمجرد النظر في قوانين نيوتن؛ إذ ينص القانون الأول على أن الجسم الساكن يبقى ساكنا ما لم تؤثّر فيه قوة ما، والجسم المتحرك يبقى متحركا بسرعة متجهة ثابتة ما لم تؤثّر فيه قوة ما، لكن إذا تحرك الجسم بالنسبة إلى إطار قصوري، فإنه يتحرك بالنسبة إلى جميع الأطر القصورية. ويربط القانون الثاني بين التسارع والقوة، لكن لأن التسارع هو «معدَّل التغيير» في الحركة، فإن تسارع الجسم لا يتغير في أي إطار قصوري.
ما نحتاج إليه إذن لممارسة الفيزياء هو إطار قصوري بشكل أو بآخر. وبناءً على أحد هذه الأطر، يمكننا إنشاء عدد لا حصر له من هذه الأطر، لكننا لا نحتاج إلى معرفة أي من هذه الأطر هو إطار السكون، ونحن لا نستطيع أن نعرف ذلك بالفعل؛ بسبب مبدأ النسبية.
لنرجع الآن إلى أحجية كيفية اكتشاف الحركة المطلقة (بما أننا لا نستطيع رؤية الأطر القصورية أكثر مما يمكننا رؤية المكان المطلق). يوضح المثال الذي ضربه نيوتن بالكُرَتَين أننا نستطيع تحديد ما إذا كان أحد الأجسام يدور أم لا، بالنظر إلى درجات الشد الداخلي به. (لاحظ أن الدوران لا يتأثر بتغيُّرات السرعة المتَّجهة المطلقة؛ ومن ثمَّ إذا كان الجسم يدور بالنسبة إلى إطار قصوري، فإنه يدور بالنسبة إلى جميع الأطر القصورية). وهذه الطريقة لا تصلح إلا لأننا نفترض ميكانيكا نيوتن مسبقًا. بمعنى أننا لا نعرف أنه يوجد في السلسلة إلا لأن النظرية تخبرنا بأنه سيوجد شد في السلسلة. يتمثل المبدأ العام فيما يلي: سنتوصل إلى الحركات المطلقة من خلال النظر إلى الحركات النسبية، ثم نسأل أنفسنا ما يلي: ما الذي يجب أن تكون عليه حركة إطار قصوري بالنسبة إلى كل هذه الأجسام، بما يجعل حركاتها النسبية إلى ذلك الإطار تتطابق مع قوانين نيوتن؟ نعرف أن العملية لن تعطينا إطارًا قصوريًا محددًا بسبب مبدأ النسبية، لكننا نرجو مع توفر نظام معقد بما يكفي أن تعطينا العملية خيارًا محددًا يشمل «مجموعة من حالات زيادة السرعة المتجهة المنتظمة»؛ أو بعبارة أخرى تعطينا مجموعة الأطر القصورية بأكملها، وإن لم تحدد إطارًا واحدًا كما كنا سنفضّل.
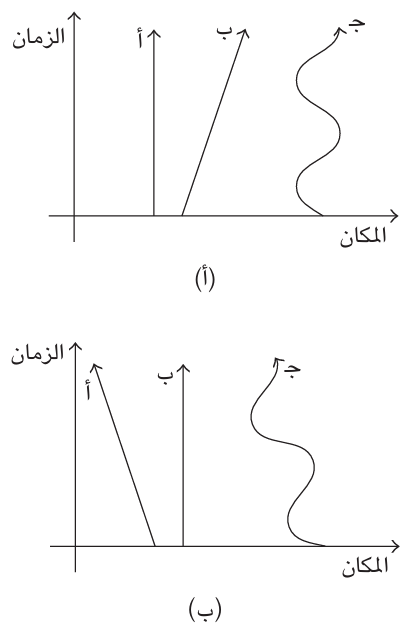
شكل 2-1: الحركة في إطارين قصوريَّين: (أ) الحركة في الإطار القصوري للجسيم «أ»؛ (ب) الحركة في الإطار القصوري للجسيم «ب».
يصوّر الشكل 2-1 هذه العملية. ففي الجزء (أ) من الشكل 2-1، تظهر حركات الجسيمات الثلاثة «أ» و«ب» و«ج» بالنسبة إلى إطار قصوري؛ حيث الجسيم «أ» في حالة سكون، بينما يتحرك الجسيم «ب» في خط مستقيم وبسرعة ثابتة، ويتأرجح الجسيم «ج» من جانب إلى آخر، ولكنه لا ينتقل بشكل منهجي إلى أي مكان. وفي الجزء (ب) من الشكل 2-1، نرى إعادة تصوير للموقف نفسه في اطار قصوري؛ حيث الجسيم «ب» فقي حالة سكون، والجسيم «أ» هو الذي يتحرك بشكل مستقيم وبسرعة ثابتة، بينما يستمر الجسيم «جـ» في التأرجح، لكنه ينجرف الان جهة اليسار.يختلف الاطاران القصوريان في أي الجسيمات هو السكان وأيه المتحرك، لكنهما يتفقان ان الجسيم «أ» والجسيم «ب» يتحركان تحركا قصوريا دون الجسيم «جـ».
ومن هذا المنطلق، يمكننا إعادة صياغة قانون نيوتن الاول على النحو التالي:
قانون نيوتن الاول (نسخة المكان المطلق): يتحرك الجسم في خط مستقيم وبسرعة ثابتة بالنسبة الى أي إطار مرجع ي قصوري ما لم تؤثر عليه قوة ما.