
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
استخدام قانون نيوتن الثاني لتحليل سلسلة من الأمثلة
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 100 – ص 105
2024-09-16
407
مثال 3–8 (مقياس عجلة بسيط). عُلِّقَتْ كتلة m بواسطة وتر من سقف عربة سكة حديد متسارعة (شكل 3–7). الوتر يصنع زاوية θ ثابتة مع الرأسي. احسب عجلة عربة سكة الحديد.
يحصل معظم الطلاب على إجابة صحيحة لهذه المسألة، لكنَّ كثيرين يستخدمون براهين مريبة مشكوكا فيها، وتؤدي بالتأكيد إلى لبس عند تطبيقها على حالات أكثر تعقيدًا. هذه ليست مسألة استاتيكا الكتلة m ليست في حالة اتزان؛ فإن لها نفس عجلة القطار. إذا أدخلنا المحورين المتصلين بالأرض المحور x الأفقي، والمحور y الرأسي)، فإن ax = a و0 = ay. شكل 3–7 (ب) يوضّح القوتين المؤثرتين على الكتلة m بواسطة كلَّ من الكرة الأرضية والوتر. المركبتان x وy للقوة  تعطيان:
تعطيان:
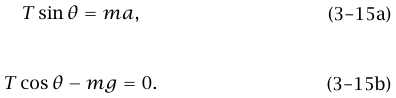
بحذف T نحصل على tan θ = a/g أو θ a = g tan.
كثير من الطلاب يستخدمون محاور متصلة بعربة السكة الحديد ويحاولون استخدام قانون نيوتن الأول ؛ لأن الكتلة m ليست متسارعة بالنسبة لهذه المحاور. إلا أن هذه المحاور ليست إطارًا قصوريًا، ولن يكون قانون نيوتن الأول صحيحًا في إطار الإسناد هذا ما لم نعدل تعريفنا للقوة ليشمل قوةً احتكاكية من النوع المحدد بدقة. «القوة» الثالثة، التي يجب إضافتها إلى شكل 3–7(ب) لكي يتلاشى حاصل الجمع المتجهي للثلاث قوى، تتجه أفقيا إلى اليسار ومقدارها ma (متجهيًّا، «القوة» الثالثة هي
؛ لأن الكتلة m ليست متسارعة بالنسبة لهذه المحاور. إلا أن هذه المحاور ليست إطارًا قصوريًا، ولن يكون قانون نيوتن الأول صحيحًا في إطار الإسناد هذا ما لم نعدل تعريفنا للقوة ليشمل قوةً احتكاكية من النوع المحدد بدقة. «القوة» الثالثة، التي يجب إضافتها إلى شكل 3–7(ب) لكي يتلاشى حاصل الجمع المتجهي للثلاث قوى، تتجه أفقيا إلى اليسار ومقدارها ma (متجهيًّا، «القوة» الثالثة هي ). يستطيع المرء أن يحصل على المعادلتين (3–15 a) و(3–15 b) إذا أدخل هذه «القوة» الإضافية، ثم استعمل قانون نيوتن الأول، إلا أن هذه «القوة» لا يمكن تفسيرها على أنها دفع أو سحب تؤثر بهما كتلة مادية أخرى على m. ومع أنه من المفيد أحيانًا، في مستوى متقدم، استخدام محاور ليست إطارًا قصوريًا، وإدخال قوى وهمية مناسبة، فإننا نعترض بشدة على استخدام مثل هذه المحاور في مقرر تمهيدي.
). يستطيع المرء أن يحصل على المعادلتين (3–15 a) و(3–15 b) إذا أدخل هذه «القوة» الإضافية، ثم استعمل قانون نيوتن الأول، إلا أن هذه «القوة» لا يمكن تفسيرها على أنها دفع أو سحب تؤثر بهما كتلة مادية أخرى على m. ومع أنه من المفيد أحيانًا، في مستوى متقدم، استخدام محاور ليست إطارًا قصوريًا، وإدخال قوى وهمية مناسبة، فإننا نعترض بشدة على استخدام مثل هذه المحاور في مقرر تمهيدي.
مثال 3–9 ( مثال لاحتكاك في اتجاه حركة) صندوق يزن 200 نيوتن (N) يستقر على أرضية عربة شحن شكل 3–8 معاملا الاحتكاك الاستاتيكي والحركي بين الصندوق والأرضية هما 0.2 = μs و0.1 = μk. افترض أن عربة الشحن كانت في البداية ساكنة، ثم تسارعت بعجلة ثابتة A = 0.65 m/s2. احسب عجلة الصندوق والقوة التي تؤثّر بها الأرضية على الصندوق. أجب عن نفس السؤالين عندما تكون عجلة عربة الشحن A = 2.5 m/s2.
من المهم أن يكون لدينا فَهم كيفي لهذه المسألة قبل كتابة المعادلات. نعلم من الخبرة أنه إذا كان مقدار العجلة A لعربة الشحن صغيرًا بدرجة كافية، فإن الصندوق لن ينزلق، ولهذا ستكون عجلة الصندوق أيضًا هي 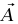 .
.
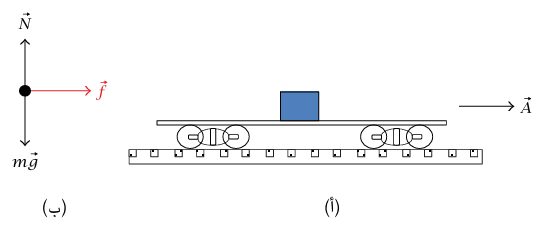
شكل 3–8: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–9.
القوة الأفقية الوحيدة المؤثرة على الصندوق هي قوة الاحتكاك التي تبذلها الأرضية عليه. هذه القوة يجب أن تتجه إلى الأمام (إلى اليمين في شكل 3–8(ب))، ويجب (لكي تستوفي شروط قانون نيوتن الثاني) أن يكون مقدارها مساويًا لكتلة الصندوق مضروبة في عجلته. إذا كانت A أكبر من قيمة معينة حرجة، فإن القوة الاحتكاكية اللازمة ستكون أكبر من أقصى قوة ممكنة للاحتكاك الاستاتيكي، وسوف ينزلق الصندوق، وستظل الأرضية أثناء الانزلاق تؤثر عليه بقوة أمامية (لأن الصندوق متحرك إلى الوراء بالنسبة للأرضية). هذه القوة، التي يمكن حسابها باستخدام قانون الاحتكاك الحركي (المعادلة (14–2))، سوف تحدد عجلة الصندوق (التي سوف تتجه إلى الأمام، ولكن سيكون مقدارها أصغر من A).
نريد أولا أن نعرف ما إذا كان الصندوق متسارعًا مع عربة الشحن أم منزلقًا؛ ولذلك يجب أن تحسب قيمة العجلة الحرجة A0. إذا كانت A < A0 فإن عجلة الصندوق تكون A، ونحصل من قانون نيوتن الثاني على f = mA؛ حيث f هي القوة الاحتكاكية التي تبذلها الأرضية، وm هي كتلة الصندوق. وحيث إن الصندوق ليست له عجلة في الاتجاه الرأسي، فيكون لدينا 0 = N – mg، وبهذا يكون f/N = A/g. لكن قانون الاحتكاك الاستاتيكي ينص على أن f/N ≤ μs وبناء على ذلك نجد أن الانزلاق يحدث إذا كانت A أكبر من القيمة الحرجة μs g = A0. باعتبار g = 9.8 m/s2 نجد أن A0 = 2(9.8) = 1.96 m/s2 (لاحظ أن A0 لا تعتمد على كتلة الصندوق)؛ لهذا يكون للصندوق نفس عجلة عربة الشحن عندما تكون A = 0.65 m/s2، وينزلق الصندوق عندما تكون A = 2.5 m/s2.
وبالتالي، عندما تكون A = 0.65 m/s2، تكون عجلة الصندوق 0.65 m/s2، وتكون القوة الاحتكاكية هي:
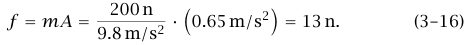
عندما تكون A > A0 تكون القوة الاحتكاكية f = μk N = μk mg. تستنتج عجلة الصندوق a من قانون نيوتن الثاني ma = f، الذي يعطي a = μk g. وبهذا، عندما يكون A = 2.5 m/s2. نجد أن عجلة الصندوق هي a = (0.1) (9.8 m/s2) = 0.98 m/s2 (مرةً ثانيةً لا تعتمد على كتلة الصندوق). القوة الاحتكاكية هي:
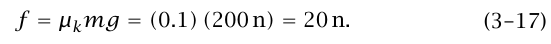
لاحظ أنه عندما تكون A > A0 فإن عجلة الصندوق والقوة الاحتكاكية لا تعتمدان على A.
مثال 3–10 (كتلتان بينهما احتكاك متبادل مسحوبتان بثالثة على سطح أملس). اعتبر الجهاز المبين في شكل 3–9 (أ)؛ حيث m1 على سطح أفقي أملس، ومعاملا الاحتكاك بين m1 وm2 هما 0.2 =μs و0.1 =μk. لكل قيم m3، نرغب في إيجاد عجلة m1، وعجلة m2، والشد في الوتر، والقوة الأفقية التي تؤثر بها m1 على m2. هذا المثال نسخة معقدة قليلًا من المثال .3–9 نتوقع أن يكون لكلٌّ من m1 وm2 نفس العجلة، إذا كانت m3 صغيرة بدرجة كافية، لكن إذا كانت m3 أكبر من قيمة حرجة معينة، فإن الكتلة الأعلى (m2) سوف تنزلق إننا بحاجة ملحة من الآن لأن نوضح أن الشد في الوتر لا يساوي m3g (خطأ شائع)؛ إذا كان الشد في الوتر m3g فإن m3 ستكون في حالة اتزان ولن تتسارع.
لنعتبر متجه وحدة 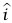 يشير أفقيًّا إلى اليمين، ومتجه وحدة
يشير أفقيًّا إلى اليمين، ومتجه وحدة  يشير رأسيًا إلى أعلى، ونعرف عجلة m1 بأنها
يشير رأسيًا إلى أعلى، ونعرف عجلة m1 بأنها 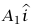 وعجلة m2 بأنها
وعجلة m2 بأنها 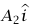 . وبفرض أن الوتر غير قابل للمط، تكون عجلة m3 هي
. وبفرض أن الوتر غير قابل للمط، تكون عجلة m3 هي 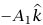 . لقد اعتبرنا متجهي الوحدة فقط لتحاشي أخطاء الإشارات، وعلى القارئ من الآن أن يكون قادرًا على الاستغناء عنهما. يوضح شكل 3–9 (ب)، (ج)، (د) مخططات بيانية لجسم حر للكتل الثلاث.
. لقد اعتبرنا متجهي الوحدة فقط لتحاشي أخطاء الإشارات، وعلى القارئ من الآن أن يكون قادرًا على الاستغناء عنهما. يوضح شكل 3–9 (ب)، (ج)، (د) مخططات بيانية لجسم حر للكتل الثلاث.
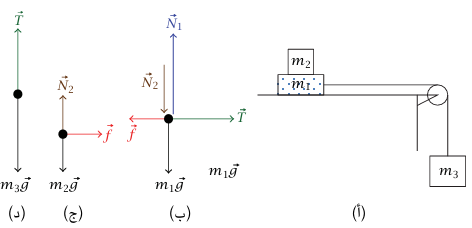
شکل 3–9: رسم توضيحي (أ) للمثال ،3–10، ومخطط الجسم الحر للكتلة m1 (ب)، والكتلة m2 (ج)، والكتلة m3 (د).
N2 هو مقدار القوة العمودية التي تبذلها إحدى الكتلتين على الأخرى، و f هو مقدار القوة الاحتكاكية، وN1 هو مقدار القوة العمودية التي تؤثّر بها المنضدة على الكتلة السفلى. ونظرًا لعدم وجود عجلة رأسية لأي من m1 أو m2، فإننا نجد (من شكل 3–9 (ج)) أن N2 = m2g و(من شكل 3–9 (ب)) أن N1 = (m1 + m2) g.
تطبيق قانون نيوتن الثاني على كل كتلة يعطي:
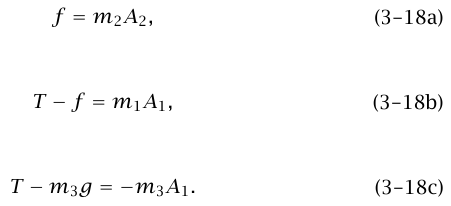
لننظر أولا إلى حالة m1 وm2 عندما يكون لهما نفس العجلة (A1 = A2). بإضافة المعادلتين (3–18 a) و(3–18 b) نحصل على 1A (m2 + T = (m1 (التي يمكن الحصول عليها أيضًا بتطبيق قانون نيوتن الثاني على الجسم المركب من الكتلتين).
بالتعويض عن T في المعادلة (c 18–3) نجد أن (A1 = gm3/(m1 + m2 + m3. وتُعطى القوة الاحتكاكية بالمعادلة:
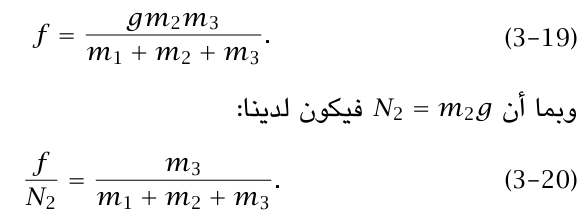
هذا الحل متوافق مع قانون الاحتكاك الاستاتيكي، بشرط أن يكون f/N2 ≤ μs. إذا كان 0.2 = μs فإننا نستطيع إيجاد قيمة m3 الحرجة بوضع 0.2 = f/N2؛ وبهذا نجد أن 0.2 ≤ 2N/f إذا كان (m2 + m3 ≤ 0.25 (m1.
لاحظ أن الطرف الأيمن للمعادلة (3–20) يكون دائمًا أقل من 1؛ ولهذا فإنه في حالة μs ≥ 1، لا يمكن أبدًا أن تنزلق m2 بالنسبة إلى m1 مهما زادت قيمة m3. إذا كان μs < 1 فإن قيمة m3 الحرجة (الناتجة بوضع f/N2 = μs) تكون μs (m1 + m2)/(1 – μs) = m3، التي تتفق مع النتيجة السابقة عندما يكون μs = 0.2.
إذا كانت (m3 > 0.25 (m1 + m2 ، فإن m2 تنزلق بالنسبة إلى m1. تُعطى القوة الاحتكاكية f بقانون الاحتكاك الحركي (f = 0.1 (m2g، ومن المعادلة (a 18–3) نجد أن g 0.1 = A2. نستطيع الآن حل المعادلة (b 18–3)، والمعادلة (c 18–3) لإيجاد المجهولين A1 وT، ونحصل على:
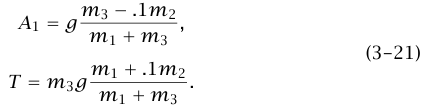
على القارئ الذي يستهويه هذا النوع من المسائل أن يتولى بنفسه ربط الوتر بالكتلة 2m بدلا من m1، أو يقوم بإدخال احتكاك عند سطح التلامس بين المنضدة وm1.