الميكانيكا الكلاسيكية مقدمة أساسيةعلى عكس التصادمات المرنة أحادية البعد الحالة النهائية في تصادم مرن ثنائي البعد لا تحدد فقط عن طريق حفظ الطاقة وكمية التحرك. هناك أربع كميات مجهولة في الحالة النهائية (المركبتان x وy للسرعتين 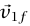 و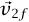 أو مقدار السرعتين واتجاهاهما). حفظ المركبتين x وy لكمية التحرك يفرض شرطين وحفظ الطاقة يفرض شرطًا ثالثا؛ وبناءً على ذلك يوجد بارامتر حرٌّ واحد في الحالة النهائية. على سبيل المثال، إذا حددنا اتجاه 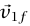، فإنه يُحدِّد مقدار  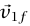ومقدار واتجاه 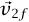. ما المعلومات الإضافية (زيادة على متجهي السرعة الابتدائية) التي يجب أن تتوفر لدينا بشأن الحالة الابتدائية لكي نتوقع الحالة النهائية تمامًا؟ للتبسيط، دعنا نفترض أن m₂ كانت ساكنة في البداية وأن الجسمين المتصادمين هما قرصا هوكي الجليد. في شكل 5–15(أ) و(ب)، الكرة رقم 1 لها نفس السرعة، ولكن الحالتين النهائيتين في كلٌّ من الموقفين هنا سوف تختلفان. في (أ) التصادم مباشر (مستقيم)، بينما في (ب) الكرة رقم 1 تتصادم تصادمًا غير مباشر مع رقم 2. ولوصف الحالة الابتدائية تمامًا يجب أن نحدد إلى أي حد من الصواب استهدفت رقم 1 عند رقم 2. يتم هذا عادةً بإعطاء قيمة بارامتر الصدم b (انظر شكل 5–15)، وهو مقدار المسافة من مركز رقم 2 التي سوف يخطئها مركز رقم 1 إذا لم تنحرف الكرة رقم 1. قد يجد القارئ المهتم أنه من المفيد حساب  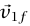و 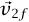 بدلالة  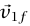وبارامتر الصدم، لكننا نحذف الحساب هنا الفكرة الدليلية هي أنه إذا كان سطحا الكرتين أملسين، فإن اتجاه  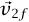(أي اتجاه الدفع المعطى للكرة رقم 2) يكون بطول الخط من مركز رقم 1 إلى مركز رقم 2 في لحظة تلامس الكرتين. في البعد الواحد يكون اللاعبان بارعين تمامًا في الرماية؛ أي إن بارامتر الصدم يساوي صفرا دائما.

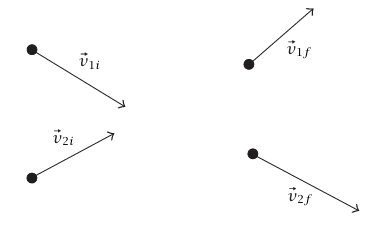
شكل 5–14: تصادم مرن في بعدين.

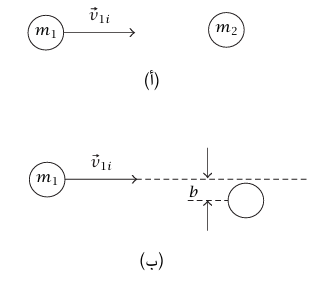
شكل 5–15: تصادم جسمين لهما بارامتر صدم.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل