
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الاندماج النووي في المختبر
المؤلف:
جوزف فايس
المصدر:
الاندماج النووي
الجزء والصفحة:
ص12-14
2025-01-14
874
لنحاول تحديد الظروف التي ينبغي أن تتحقق عمليًّا للتمكّن من الاستفادة من تفاعلات الاندماج النووي. أولا: ما الذرات الخفيفة التي ينبغي أن نستخدمها؟ تبين التجارب التي أجريت في المختبرات لتصادم الذرّات أن أسهل تفاعل اندماج يمكن إجراؤه يكون باستخدام نوعين من الهيدروجين الدوتريوم والترتيوم، وهما في الواقع نظيران للهيدروجين؛ إذ يكتب التفاعل كما يلي:
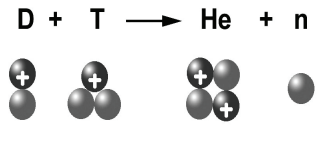
وقد بينا بصورة يسيرة، تحت رموز العناصر الكيميائية، نوى الذرات المعنية؛ فعلى يسار السهم، أي قبل حدوث التفاعل، نلاحظ نوى الدوتريوم والترتيوم المكونين من جسيم إيجابي واحد (البروتون) وعلى التوالي نترون ونترونان، علما أن النترون هو جسيم متعادل ذو كتلة قريبة جدا من كتلة البروتون، وعلى يمين السهم يتمثل الناتج من تفاعل الاندماج؛ إذ لدينا ذرة هيليوم (بروتونان) ونترونان) إضافة إلى نترون حرّ. الجدير بالذكر
أن محصلة ناتج هذا التفاعل من الطاقة يكون إيجابيا؛ ذلك أنه إذا عددنا طاقة ذرات الدوتريوم والترتيوم مساوية لـ 2 (1 للدوتريوم و اللترتيوم المتعادلين في درجة الحرارة )، فإن طاقة ذرّة الهيليوم تساوي 37 وطاقة النترون الحر تعادل 140؛ أي أننا حققنا مكسبا يناهز الـ 100 في الطاقة،
بموازنة طاقة جسيمات ما قبل التفاعل مع طاقة الجسيمات الناتجة. وقد عينت تجارب الاصطدام الذري الذرات الأكثر إثارة للاهتمام في هذا السياق، لكنها بينت لنا في الوقت ذاته أنه لا ينبغي توقع إنتاج الطاقة بمجرد إطلاق شعاع من الوتريوم مباشرة على الترتيوم المستهدف البارد؛ ففي أكثر من %99 من الحالات، يكبح الجسيم الملقى حتى يثْنى عن التفاعل؛ فحالات التصادم العادية مع الانحراف والتباطؤ أكثر شيوعا من حالات التصادم المسفرة عن اندماج نوى الذرات. بيد أن النتيجة تختلف تمامًا في حال غاز ساخن مكوّن من خليط متعادل من الدوتريوم والترتيوم؛ إذ لا تفقد عندئذ الطاقة لدى التصادم، بل تتبادلها الأيونات المكونة للمادة السريعة الاشتعال، فتسفر الأيونات عن العديد من حالات الاصطدام الأخرى في الغاز ذاته، ومنها ما يمكن أن يكون مواتيا لعملية الاندماج، الجدير بالذكر أنه لا بد من أن تندمج النوى في قلب الغاز الساخن؛ لذلك تعرف هذه العملية بالاندماج النووي الحراري، وهكذا يتجلى شرط أساسي من شروط هذه العملية؛ ذلك أن تفاعلات الاندماج لا يمكن أن تتم إلا مع أيونات ذات سرعة كافية؛ لذا فمن الضرورة ألا تفقد هذه الجسيمات إثر عمليات أخرى قدرًا مفرطًا من الطاقة طوال الاصطدامات المثمرة. بمعنى آخر وأكثر يسرا لا ينبغي أن يبرد المزيج الغازي بسرعة مفرطة. لا بد هنا من توخي المزيد من الدقة؛ فبعد تفاعل الاندماج يواجه أيون الهيليوم مصيرًا مختلفا تماما عن مصير النترون؛ فالنترون الصغير الحجم، والمجرّد من الشحنة الكهربائية، سرعان ما يغادر - وبخط مستقيم - البلازما التي لا يتفاعل معها عمليا، إلا أن طاقته لا تتبدد؛ بل تسترد في صورة حرارة في الجدار المادي؛ إذ سيمتص . أما الهيليوم، فهو أيون، لذلك سيتفاعل، خلافًا للنترون، وبشدة مع إلكترونات وأيونات البلازما، ونظرا لكون الهيليوم هو الأيون ذو الطاقة الكبرى، فهو الذي سيتخلى شيئًا فشيئًا عن طاقته للجسيمات الأكثر برودة – والتي يصادفها، تفاعلات الاندماج إذن - كما في النجوم - مصدر للحرارة في قلب البلازما ذاتها.
مما لا شك فيه أننا نسعى إلى بلوغ حالة يعوّض فيها مصدر هذه الطاقة الداخلية؛ أي أيونات الهيليوم الخسائر كافة، التي لا مفر للبلازما من تكبدها، وهي الحالة المسماة الإشعال أي حالة دائمة من الاشتعال تستمر ما استمرت تغذيتها بالوقود الظروف التي ينبغي توافرها لبلوغ هذه الحالة ليست عسيرة، وقد أسفرت الحسابات عن معادلة يسيرة تعرف بمعيار الإشعال (وهي معادلة قريبة جدا من معادلة أخرى أقدم شرط لاوسون) .
عند = T 100 ميلون درجة ، ينبغي 1020<xN
n× لكل م ولكل ث؛ إذ :
Nهي الكثافة وتقاس بعدد الجسيمات لكل متر مكعب كلما ازدادت الكثافة زاد عدد الاصطدامات في كل ثانية)، وτ (ثوان) هي الزمن
النموذجي لتبريد بلازما الدوتريوم والترتيوم، الذي يعرف عمومًا بزمن الطاقة. حصر تعد هذه المعادلة - على الأقل من حيث المبدأ - بديهية إلى حد ما؛ فهي تنص بصورة يسيرة على أنه كلما قصر الزمن الذي يبقى فيه الوسط ساخنا زاد العدد المطلوب من التصادمات لكلِّ ثانية، علما أن القيمة الرقمية للعدد الثاني - هنا نقيم في الواقع حاجزاً عملياً لا بد من تخطيه هو حاجز سرعان ما ندرك مدى ارتفاعه، فليس من السهل الحصول على وسط يحدث فيه الاندماج النووي.
 الاكثر قراءة في مواضيع عامة في الفيزياء النووية
الاكثر قراءة في مواضيع عامة في الفيزياء النووية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















