EVIDENCE  OF  WAVE  PROPERTIES IN  ELECTRONS

There is much evidence to support the fact that particles such as electrons can and do exhibit wave behavior. Consider the traditional optical principle of diffraction, which conclusively demonstrated the wave property of light. In Young’s time honored experiment, a light beam is incident on a target with two parallel slits (Figure 1.1). A pattern forms on a screen after the slits. The pattern clearly shows diffraction occurring when light passing through each slit interferes, to form the fringes. It was deduced that light does this because it is a wave and waves interfere in this manner. If light were a particle, there is no way that particles passing through the slits could produce this pattern. In 1928, physicist G. P. Thomson attempted the same experiment, with electrons instead of light. Using electrons accelerated by high voltage, he produced a collimated beam of electrons with a deBroglie wavelength of 0.01 nm. This is a much

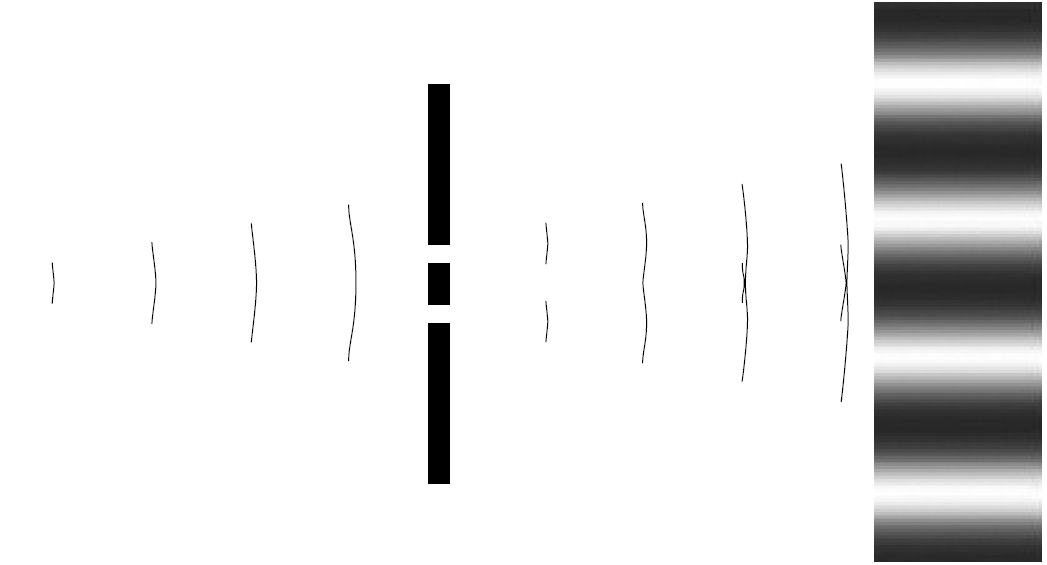
Figure 1.1. Young’s double-slit experiment.

shorter wavelength than light, so smaller slits would be needed. In his experiment he utilized extremely thin gold foil as a crystal, which would diffract the electron beam as it passed through. The pattern produced was a striking circular diffraction pattern showing without a doubt that electrons were diffracting and hence exhibiting wave behavior. Furthermore, it was shown that magnetic and electrical fields would affect the pattern, proving that the particle exiting the foil was indeed a charged electron. It is important to understand that in the electron double slit experiment, that diffraction pattern is still produced even when the beam of electrons is made so weak that only one electron is allowed to pass through the slit at one time. If the electron was “just a particle,” one would expect that it passes through one slit or the other but never both, giving a simple pattern consisting of two areas on the detection screen. When more than two areas (indeed, when an interference pattern) are seen, we know that even individual electrons pass through both slits simultaneously. Only a wave is capable of such behavior. Since the time of Thomson’s original experiment, others have reproduced Young’s double-slit experiment using electrons instead of light. The slits are very close together, on the order of 10^-6 m, which is required given the extremely short deBroglie wavelengths. When electrons pass through the slits and are expanded onto a phosphorescent screen, the resulting pattern looks exactly like that expected with light. Furthermore, electrons have been shown to refract as light does when passing through, say, the interface to a crystal (the air to crystal surface, where refractive index changes). Unmistakably, the electrons, normally considered a particle with mass, are exhibiting wave behavior! Quantum mechanics exploits this wave behavior by describing the energies of electrons in the atom (the electrons that create light in making the jump between allowed levels) using wave mechanics. Erwin Schrodinger devised the famous wave equation bearing his name, which describes the states of a bound electron and allowed computation of possible energy levels. The electron is assumed to be bound by forces within the atom, and (more or less) classical wave mechanics are applied to the electron to yield a prediction of how it behaves in this bound state (as if it were a wave). The solution of these complex wave equations yields a prediction as to the probability of finding an electron in a particular area of space around the nucleus of the atom. Unlike the classical Newtonian approach, where an electron is in an exact trajectory around the nucleus, the wave approach simply gives us a probable location for the electron.

مواضيع ذات صلة

الفزياء والكون .. ميكانيكا الكم

ميكانيكا الكم الخاصة بالروابط

ما الفائدة؟

إعادة النظر في اللامحلية

عوالم متعدّدة

هل نغيّر الفيزياء؟

الاحتمالات والقياسات

مبرهنة بيل وضرورة اللامحلية

الترابط والتشابك

الحالات الكمية والتراكب الكمي

التداخل والقياس

ألغاز الكم