WAVEFUNCTIONS  AND  THE PARTICLE  IN  A  BOX MODEL

Schrodinger’s model pictures electrons in orbit as standing waves in which the orbits are of an exact size so as to allow an electron with a waveform to occupy it in a whole number of wavelengths. As the electron orbits, it comes around and must assume exactly the same position at the end of a complete orbit as it did at the beginning of that orbit (i.e., only an integral number of waves fit inside the orbit). If an electron acquires more energy, its wavelength decreases slightly and it no longer fits inside the orbit. The ground state is now defined as the point where an electron has just enough energy so that a single wave fits inside the orbit. Using this model, one may compute the allowed energy levels of these standing waves and hence the allowed energy levels of the electron. Let us now model the electron as a particle in a box, as in Figure 1.1. The sides of the box represent energy potentials that confine the electron. If we assume Schrodinger’s theory that the electron must exist as a standing wave inside this box to be correct, we can describe the behavior of the electron in orbit by the wave function ψ which in this case is a simple sine function of the same form as that of a simple harmonic oscillator. At the edges of the box, the wave function must be equal to zero since it is a standing wave (i.e., the wave has nodes at the box edges). By substituting integers into the wave function, we may identify many possible modes for such a wave three are shown in Figure 1.1. Each mode will have a successively higher energy and in-between modes (those that do not have an integral number of wavelengths a standing wave inside the box) cannot exist. This model fits well with observed quantizations of energy levels in atoms. We may now adapt this model to real particles such as an electron in an orbit by changing the model so that the sides are not infinite but rather are finite in height. This change allows the confined particle (an electron in this case) to leave the box, but only after acquiring significant energy: While in the box the allowed energy levels are well defined. In such a situation, energy levels are lower than in the infinite wall example above but follow the same basic structure. Finally, real particles such as an electron in orbit must be treated in three dimensions. This is quite posssible, although the mathematics becomes somewhat complex. It is important to note that this wave approach is not limited to predicting the behavior of electrons in orbit but may also be applied to the behavior of a diatomic molecule such as N₂. The nitrogen molecule may be modeled as two atoms

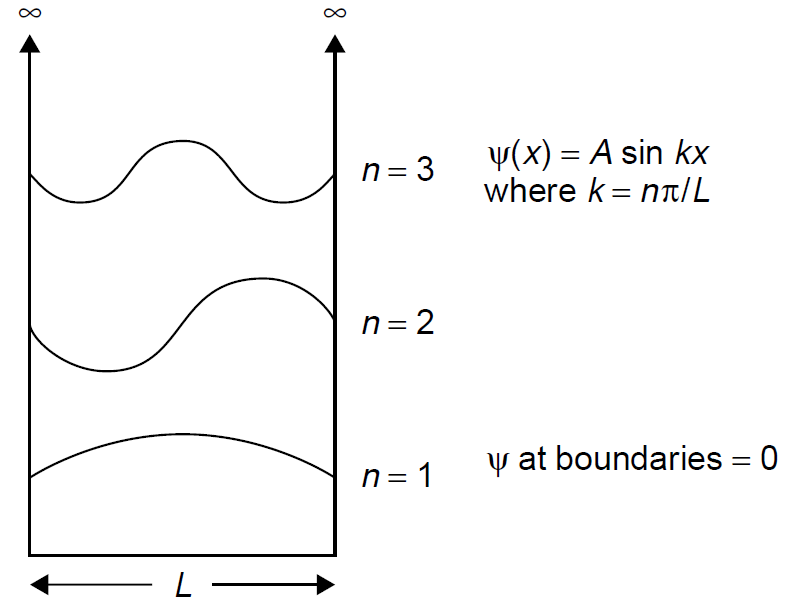
Figure 1.1. Model of a particle in a box.

connected by a spring (the bond between the individual atoms). Using an approach similar to that for the particle in a box, we may model this system as a harmonic oscillator (a quantum harmonic oscillator) to determine the energy levels allowed for such a system.

مواضيع ذات صلة

الفزياء والكون .. ميكانيكا الكم

ميكانيكا الكم الخاصة بالروابط

ما الفائدة؟

إعادة النظر في اللامحلية

عوالم متعدّدة

هل نغيّر الفيزياء؟

الاحتمالات والقياسات

مبرهنة بيل وضرورة اللامحلية

الترابط والتشابك

الحالات الكمية والتراكب الكمي

التداخل والقياس

ألغاز الكم