
Conductors and Insulators
 المؤلف:
Roger J Blin-Stoyle, FRS
المؤلف:
Roger J Blin-Stoyle, FRS
 المصدر:
Physics of Particles, Matter and the Universe
المصدر:
Physics of Particles, Matter and the Universe
 الجزء والصفحة:
p 88
الجزء والصفحة:
p 88
 24-5-2016
24-5-2016
 1648
1648
Conductors and Insulators
Was mentioned that an electric current through a metal is due to a flow of electrons. Our task now is to understand how electrons, which are held in an atom by the electrical attraction of the nucleus are able, in a metal, to escape from this attractive force. The process can most simply be understood by considering the potential well in which the atomic electrons are confined. This is shown in figure 1.1 (a) for a single atom. The attractive force due to the nucleus becomes stronger the nearer the electron is to the nucleus and, correspondingly, the potential well becomes deeper. The further the electron is away from the nucleus the weaker the force and so the well gradually levels out at large distances. In the well the horizontal lines represent the quantized energy levels in which the electrons are distributed according to the exclusion principle. When the atoms are brought very close to each other to form a solid the electrons can feel the attraction not only of their own atomic nucleus but also, to some extent, that due to neighbouring nuclei. This increased attraction therefore lowers the potential energy curve between atoms as shown in figure 1.1(b) for a small row of atoms. As an electron moves away from its nucleus its potential energy increases but, before it gets to the brim of the well as in the case of an isolated atom it begins to feel the attraction of the neighbouring nucleus and the potential energy begins to drop again. This means that the levels A and B in which an electron would be confined in an isolated atom now extend throughout the solid; they sit above the top of the row of potential wells. Of course there are many levels A and B one for each atom-and the result is a bundle of levels all with slightly different energies forming what is called a band.
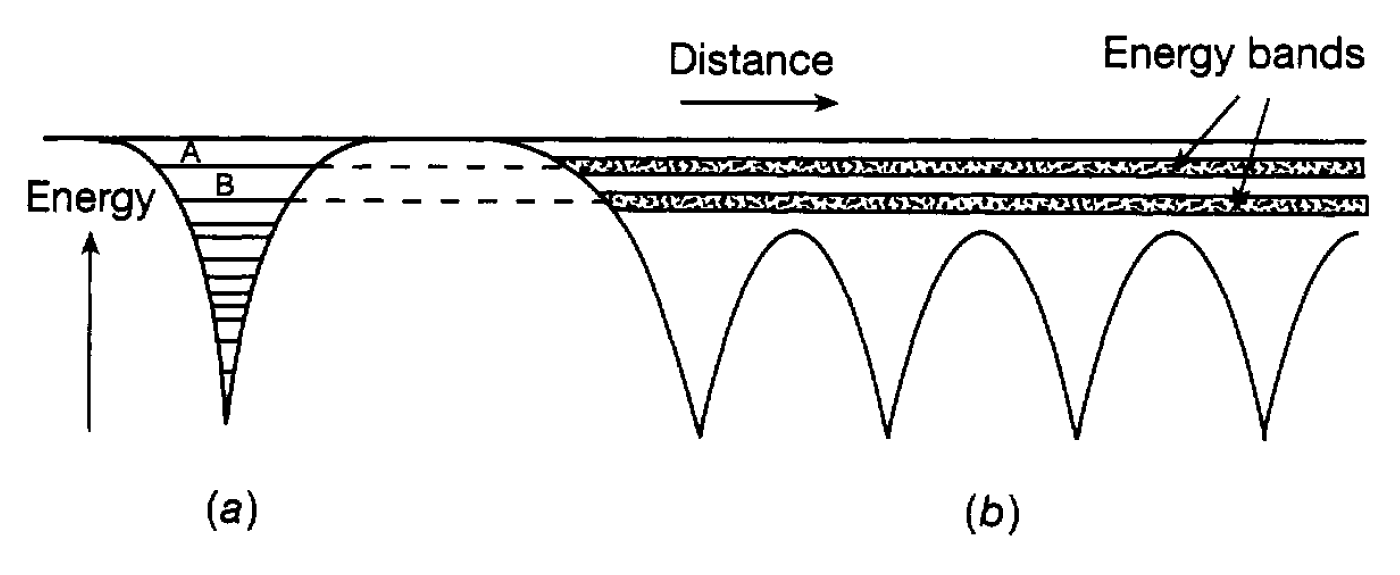
Figure 1.1: Electron potential wells: (a) a free atom; (b) atoms in a solid.
In figure 1.2(b) the bands originating in the levels A and B are shown. Sometimes such bands can be well separated, sometimes they are very close and sometimes they overlap. Consider now a solid formed from atoms for which normally there is one electron in the level B. In the solid state this electron can now move around the solid; it is no longer constrained by the potential well as in an isolated atom. Of course, each atom will contribute an electron and so there is a very large number of electrons able to undergo this movement. Each one will be in a different state within the band, as required by the exclusion principle. If not all the levels in a band are occupied (see figure 1.2(a)) then, when an electric field is applied, electrons in the band can pick up small amounts of energy and move to unoccupied levels. This means that they can move under the influence of the field and, therefore, carry an electric current. Such electrons are referred to as conduction electrons and the band as a conduction band. We have here the situation which occurs in a metal where there is always a conduction band just partially filled with electrons. It should also be mentioned here that energy can also be given to conduction electrons by a heat input and they can then carry this heat energy through the solid. This is a much more effective way of conducting heat than the passing on of atomic vibrations as described. This is why metals are much better heat conductors than non-metals.
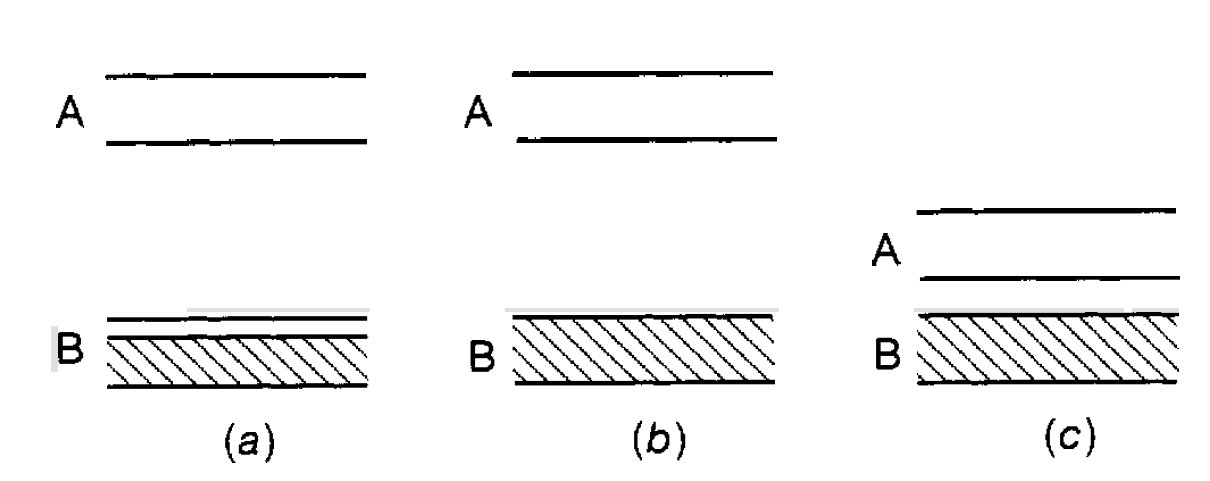
Figure 1.2: Bands A and B in (a) a conductor (unoccupied levels in band B), (b) an insulator (band B full), (c) a semiconductor (small band gap).
However, the electrons are not completely free to move. In most solids the arrangement of the component atoms is not absolutely regular; there are imperfections. There may also be impurities. In addition, the atoms are not stationary: they are oscillating in a random way about their equilibrium positions due to the thermal energy of the solid. These different effects impede the motion of the electrons and lead to the phenomenon of electric resistance. As the temperature of a metal is lowered the thermal vibrations decrease in amplitude and so it is to be expected that its resistance will also decrease; this is indeed observed experimentally. Conversely, electrons moving through a solid under the influence of an electric field (an electric current) and colliding with atoms increase the amplitude of the atomic vibrations, leading to a corresponding rise in temperature. This accounts for the heat generated in the wires of, for example, electric fires and electric light bulbs. Consider now an atom in which the level B has the full complement of electrons allowed by the exclusion principle. This means, in turn, that in the solid the band corresponding to the level B is full (see figure 1.2(b)). If an electric field is applied the only way that an electron can have more energy is for it to jump into the empty band corresponding to the level A. However, if there is a large gap between the two bands it will not have sufficient energy to do this and hence no change of electron energy can take place and no electric current can flow. This is the situation with electric insulators such as glass. Of course, if a massive electric field is applied then electrons can make the jump to the unoccupied band and current flows, leading to a breakdown of the insulator.
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


