
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Time Dilation
المؤلف:
Roger J Blin-Stoyle, FRS
المصدر:
Physics of Particles, Matter and the Universe
الجزء والصفحة:
p 107
24-5-2016
2376
Time Dilation
The foregoing discussion implies that there is nothing absolute about time. For any particular observer time appears to flow uniformly in relation to his/her frame of reference. However the time sequence of events for observers in different frames is, as we have seen, not always the same. This has a profound bearing on the measurement of time in different inertial frames. To understand this in more detail let us consider another thought experiment. Suppose the first observer measures the time taken for a light signal to be sent from him and reflected back in a mirror M fixed in his frame of reference (frame A) as shown in figure 1.1(a). The time which will have elapsed when the light has travelled to the mirror
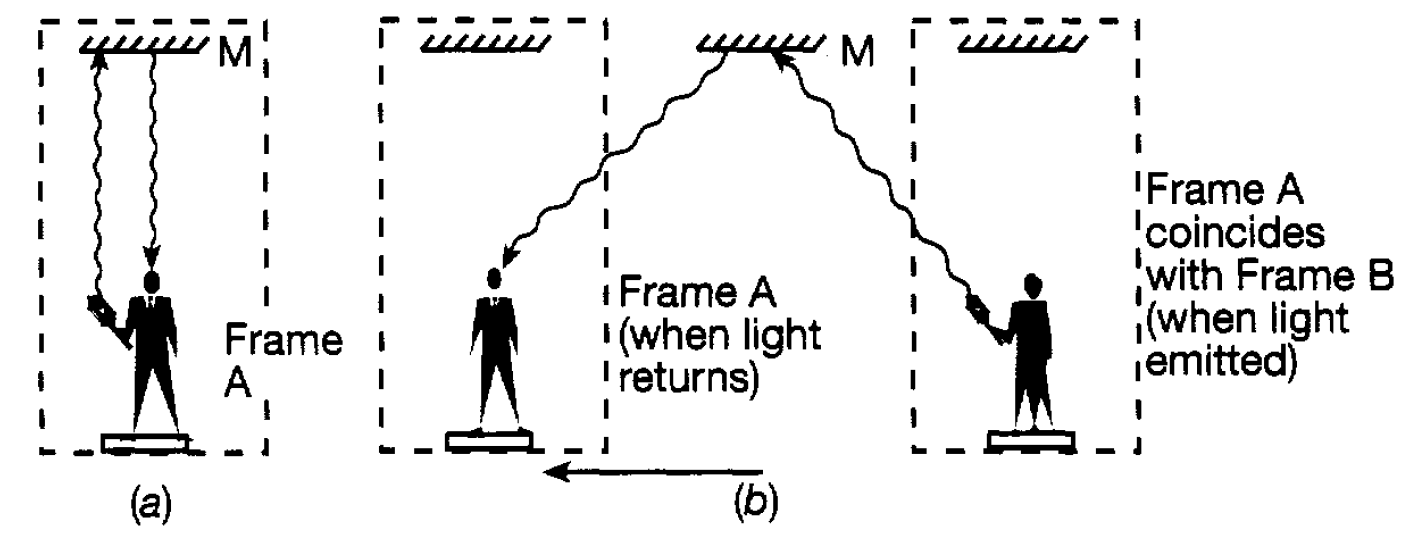
Figure 1.1 The journey of a light signal (a) with reference to the first frame, and (b) with reference to the second frame.
and back to him is simply the time taken to travel twice the distance separating him and the mirror. Now consider a second observer travelling at a uniform speed (moving to the right) relative to him. She could carry out the same measurement with an equivalent system set up in her frame of reference (frame B) and, using identical clocks, would obtain the same value for the time taken for the light to travel to and from a mirror set at the same distance from her. However, suppose she measures the time taken for the journey of the light in the frame A using the clocks in her frame of reference (B). From her point of view the mirror M in the first frame is moving with uniform speed to the left and so if she coincides in position with the first observer at the instant the light starts on its journey she will see it follow a longer path as shown in figure 1.1(b). This means that the time for the complete journey is longer when measured in relation to frame B. If the time interval for this journey were used as the ‘tick-tock’ of a clock (equivalent, for example, to the forward-backward motion of a pendulum), then the second observer would regard time as flowing more slowly in frame A than in her own (frame B) since it takes longer for a ‘tick tock’ to be completed. We have here the phenomenon of time dilation. Of course, the situation is completely symmetrical since motion is relative and the first observer, carrying out the equivalent measurment, would equally regard time as flowing more slowly in frame B. At first sight this raises a problem which is famously summarized in what has been called the twins paradox as follows. Although the foregoing discussion has been carried through by considering time in relation to processes involving light signals, the conclusions about time dilation hold generally and not simply for these specific processes. In other words, all types of clock mechanical or electrical, biological processes etc are subject to time dilation effects. These effects, however, are very small unless relative speeds near to the speed of light are involved; they have no effect on our everyday experiences. They have been demonstrated most effectively by measuring the time taken for radioactive particles to decay when at rest and when in high speed motion in the laboratory. It is found that their lifetimes in motion are increased precisely as predicted by relativity theory. Turning now to the twins paradox, this simply considers the ageing implications for a pair of twins, one of which remains on earth whilst the other makes a high speed round trip into space. Relative to the twin on earth, time will have moved more slowly (will have been dilated) for the twin in the spacecraft and the travelling twin should have aged less than the earthbound twin. However, in relation to the spacecraft’s frame of reference, it is the earth that has moved away and then returned so the travelling twin would expect the earthbound twin to have aged less. The resolution of this paradox is to recognize that the situation is not completely symmetrical. The frame of reference based on the earth is, essentially an inertial frame whilst, with reference to this frame, the spacecraft experiences accelerations during its launching, turn around and landing. The earthbound twin is always in an inertial frame whilst the travelling twin is not. Detailed considerations* then show that the first conclusion that the travelling twin has aged less is correct.
 الاكثر قراءة في النظرية النسبية الخاصة
الاكثر قراءة في النظرية النسبية الخاصة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















