
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Relativistic Quantum Mechanics
المؤلف:
Roger J Blin-Stoyle, FRS
المصدر:
Physics of Particles, Matter and the Universe
الجزء والصفحة:
p 113
24-5-2016
2397
Relativistic Quantum Mechanics
We have seen that the postulates of relativity theory have required modifications in the way in which we deal with the classical treatment of motion, energy and momentum. In particular the three space and one time dimensions turn out to be intimately related. No longer can time be simply regarded as an ‘ever flowing stream’ unrelated to spatial considerations. Indeed we are in a situation where events must be dealt with in a more general four dimensional space including time. For two inertial frames moving with uniform speed relative to each other we have seen that the four coordinates specifying spatial position and time in one frame are related to the coordinates in the other frame in a way that is more complex than obtained by simple classical considerations. It is the requirement that all physical laws should be the same in all inertial frames of reference that has led to the modifications just referred to. The resulting relativistic laws of motion are then said to be invariant under a transformation which changes the space time coordinates according to the above relations. This transformation of coordinates is referred to as the Lorentz transformation, named after a Dutch physicist who first formulated the details of the transformation. In turn, we should also expect that this invariance requirement also has implications for the theory of quantum mechanics. Here it turns out that the Schrodinger equation from which wave functions are derived is not Lorentz invariant and, therefore, if relativistic effects are to be dealt with, it has to be modified. The problem is that the Schrodinger equation a complicated differential equation is based on the classical relationship between energy and momentum, namely
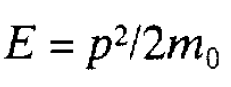
rather than the relativistic expression given in the last section. Naturally, with the advent of relativity theory, relativistic quantum mechanical wave equations were developed. Two even more complicated equations emerged. One was based directly on the relativistic expression relating energy and momentum given in the last section and is known as the Klein-Gordon Equation. The other was based on the square root of that equation, namely
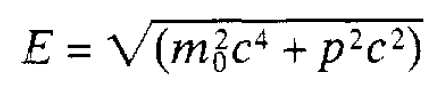
and is known as the Dirac Equation. This latter equation, which was brilliantly derived and developed by the British physicist and Nobel Laureate, Paul Dirac, led to remarkable outcomes. First, it is found that the equation only makes sense if it describes the behaviour of particles having an intrinsic spin of 4. This means that it is the natural equation to use when dealing with electrons which have spin ½: the spin of the electron is, as it were, built into the mathematics and does not have to be tacked on. Second, the magnetic properties of the electron predicted by the equation agree almost exactly with those observed. Third, the equation also has solutions for negative energies. This comes about because when the square root of an expression is taken, as above, the result can be negative as well as positive (2×2 = 4 and, also, (-2)×(-2) = 4). This raised a terrible problem because any normal electron with a positive energy would drop into one of these negative-energy states and release energy in the form of electromagnetic radiation (a photon) in just the same way that electrons emit radiation in an atom by jumping from high to low energy states. Since there is an infinite number of negative energy states with energies ranging from –m0c2 (when p was zero) downwards (as p increases) it follows that no electron could exist with positive energy; it would always fall into this bottomless pit of negative energy states. Dirac’s approach to solving this problem was to propose that every negative-energy state is occupied by an electron. In other words, so called empty space-referred to in physics as the vacuum is in fact filled with an infinite ‘sea’ of unobservable negative-energy electrons. The point of this proposal was that a positive-energy electron would then be unable to drop into a negative energy state because the Pauli exclusion principle forbids two electrons occupying the same state and the negative energy states are all occupied. The situation is illustrated in figure 1.1(a) where a single electron sits above the infinitely deep sea of occupied negative energy electron states. Here it will be noted that there is a gap of magnitude 2m0c2 which cannot be occupied by a free electron since it would imply that its rest mass was less than m0. (With p = 0, E = + m0c2 or - m0c2). This proposal then had a profound consequence. Considering only the ‘vacuum’, suppose a photon is absorbed by a negative energy electron and it is given sufficient energy (greater than 2m0c2 ) to raise it into a positive energy state as shown in figure 1.1(b). The resultant ‘hole’ in the negative-energy sea will behave as a positively charged electron as we saw when discussing holes in the context. Thus, whereas before the photon is absorbed by the negative energy electron there is just the vacuum, after the excitation there is a pair of additional particles a negatively charged electron and a positively charged
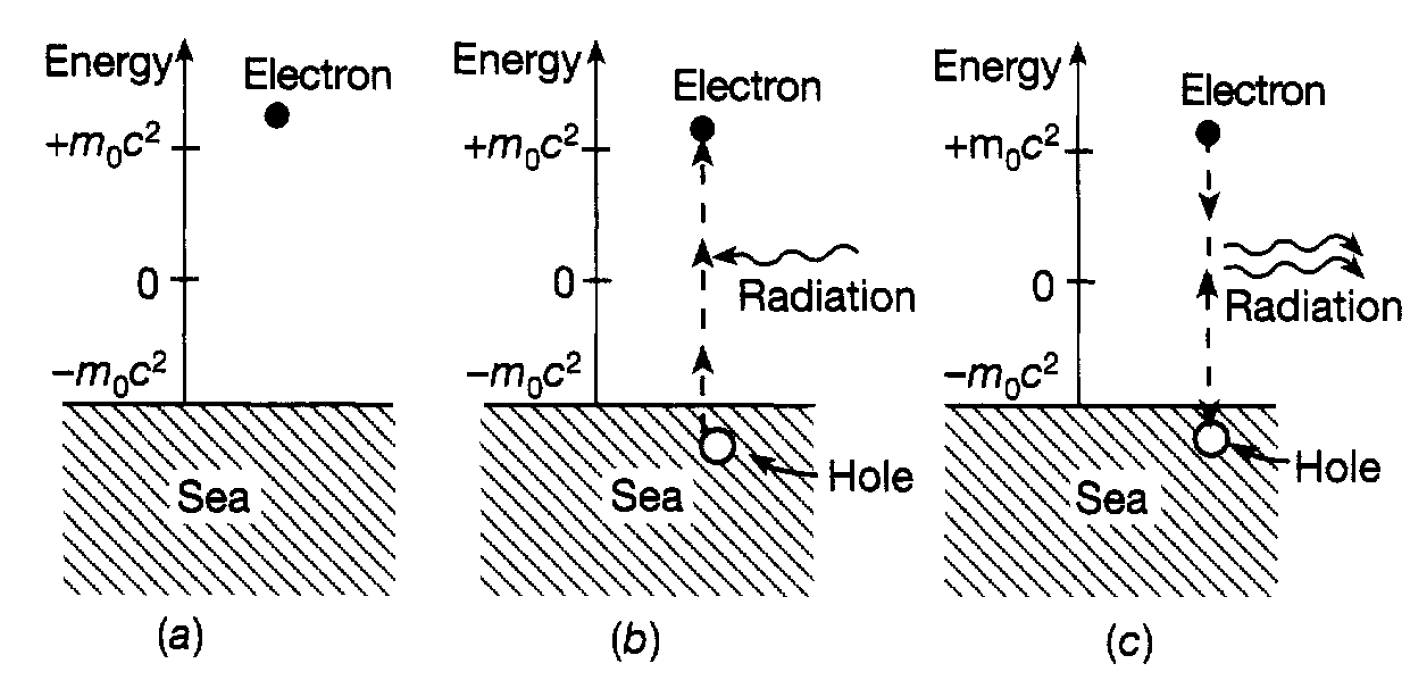
Figure 1.1: The sea of negative energy electrons. (a) With a single positive energy electron; (b) a negative energy electron excited into a positive energy state, leaving a hole; (c) the annihilation of a positive-energy electron by a hole.
‘electron’. The process is known as pair production. This latter particle is now called a positron (denoted by e+) and is one example of what are referred to as antiparticles. It has exactly the same mass as an electron and has the same spin (½) but a positive charge equal in magnitude to that of the electron. The prediction that they should exist was a tremendous triumph for Dirac when his conjecture was confirmed experimentally by Anderson in 1932 who first detected positrons in cosmic rays (particles impinging on the earth from outer space) by analysing the tracks made by them in photographic plates. Since then, pair creation and the properties of positrons have been studied in great detail in the laboratory. There is also an inverse process that can take place shown in figure 1.1(c), in which an electron falls into a hole, the released energy being carried away as electromagnetic radiation (in this case, to satisfy conservation laws, two photons are emitted). Both electron and positron disappear and this process, for obvious reasons, is known as pair annihilation. It should also be remarked that the production and annihilation of particle antiparticle pairs is continually happening in empty space. Relation connecting energy and time was mentioned for short time periods the energy is not precisely known. Energy, as it were, can be ‘borrowed’ for a while but must be handed back after the time period (l0-20s or less) has elapsed. Thus energy to create a particle antiparticle pair is available for that short period and empty space is full of these transitory pairs. The concept of an infinite sea of negative energy particles in the vacuum is clearly difficult to assimilate and, since Dirac’s original formulation, the theory of particles and antiparticles and their creation and annihilation has been considerably developed so that no longer does understanding rest on such a strange physical idea. The Dirac equation is still used to descibe particles of spin ½ but in a somewhat different way and developments in what is called quantum field theory now enable us to deal in a much neater and logical way with the creation and annihilation of particles and antiparticles without having to retain the concept of a negative energy sea of particles. Similarly, the Klein Gordon Equation is used in this context to describe particles having, for example, spin 0.
 الاكثر قراءة في مواضيع عامة في النظرية النسبية
الاكثر قراءة في مواضيع عامة في النظرية النسبية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















